Week 8: Regression Analysis

KIN 610 - Spring 2023

Ovande Furtado

Credits

Navarro and Foxcroft (2022)

Simple Linear Regression

Linear Regression Models

  • A way of measuring the relationship between two variables
  • Similar to Pearson correlation, but more powerful
  • Can be used to predict one variable from another

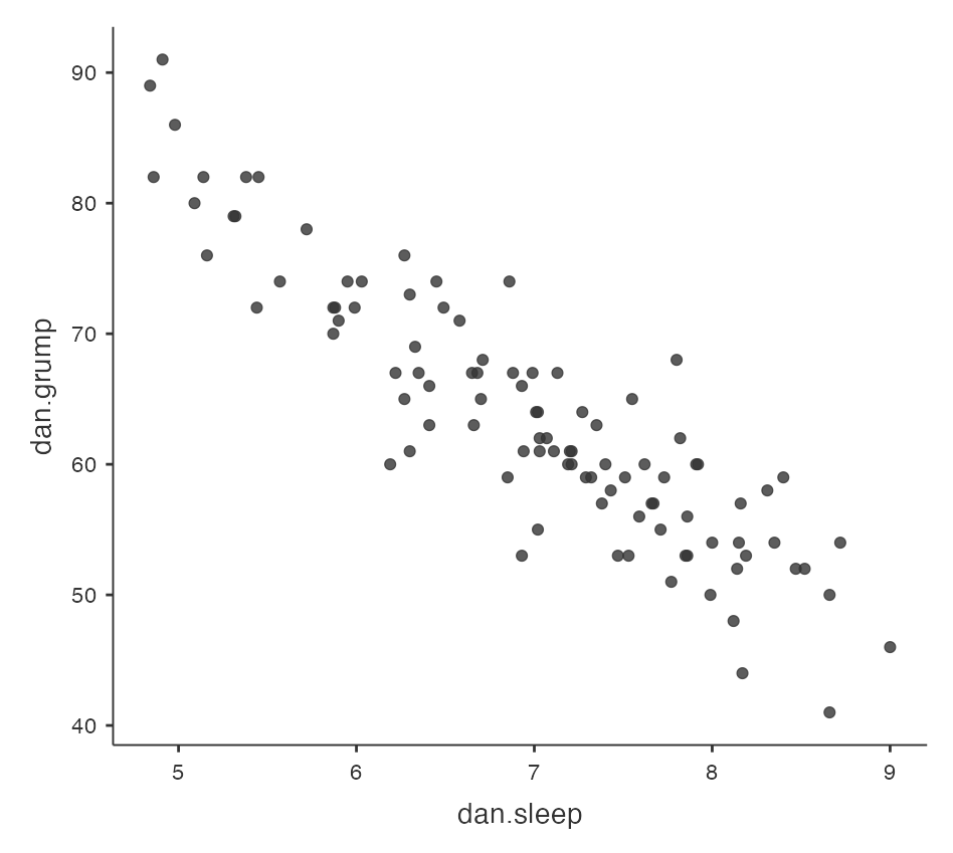
Example: Parenthood Data Set

  • Data set contains measures of sleep and grumpiness for Dani
  • Hypothesis: less sleep leads to more grumpiness
  • Scatterplot shows a strong negative correlation (r = -.90)

Regression Line

  • A straight line that best fits the data
  • Represents the average relationship between the variables
  • Can be used to estimate grumpiness from sleep

How to Draw a Regression Line?

  • The line should go through the middle of the data

  • The line should minimize the vertical distances between the data points and the line

  • The line should have a slope and an intercept that can be calculated from the data

The formula for a straight line

  • Usually written like this: \(y = a + bx\)

  • Two variables: \(x\) and \(y\)

  • Two coefficients: \(a\) and \(b\)

  • Coefficient \(a\) represents the y-intercept of the line

  • Coefficient \(b\) represents the slope of the line

The interpretation of intercept and slope

  • Intercept: the value of \(y\) that you get when \(x\) = 0
  • Slope: the change in \(y\) that you get when you increase \(x\) by 1 unit
  • Positive slope: \(y\) goes up as \(x\) goes up
  • Negative slope: \(y\) goes down as \(x\) goes up

The formula for a Regression line

  • Same as the formula for a straight line, but with some extra notation

  • So if \(y\) is the outcome variable (DV) and \(x\) is the predictor variable (IV), then:

\[\hat{y}_i = b_0 + b_1 x_i\]

\(\hat{y}_i\): the predicted value of the outcome variable (\(y\)) for observation \(i\)

\({y}_i\): the actual value of the outcome variable (\(y\)) for observation \(i\)

\({x}_i\): the value of the predictor variable (\(x\)) for observation \(i\)

\({b}_0\): the estimated intercept of the regression line

\({b}_1\): the estimated slope of the regression line

The assumptions of the regression model

  • We assume that the formula works for all observations in the data set (i.e., for all i)

  • We distinguish between the actual data \({y}_i\) and the estimate \(\hat{y}_i\) (i.e., the prediction that our regression line is making)

  • We use \(b_0\) and \(b_1\) to refer to the coefficients of the regression model

    • \(b_0\): the estimated intercept of the regression line

    • \(b_1\): the estimated slope of the regression line

Residuals of the Regression model

Code 
# Generate some example data with a strong negative correlation
set.seed(123)
x <- rnorm(100)
y <- -0.8*x + rnorm(100, sd=0.5)

# Plot the data
plot(x,y)

# Add the best fit line
abline(lm(y ~ x), col="red")

Now, we have the complete linear regression model

\[\hat{y}_i = b_0 + b_1 x_i + {e}_i\]

  • The data do not fall perfectly on the regression line

  • The difference between the model prediction and that actual data point is called a residual, and we refer to it as \({e}_i\)

  • Mathematically, the residuals are defined as \({e}_i = {y}_i - \hat{y}_i\)

  • The residuals measure how well the regression line fits the data

    • Smaller residuals: better fit
    • Larger residuals: worse fit

Estimating a linear regression model

  • We want to find the regression line that fits the data best

  • We can measure how well the regression line fits the data by looking at the residuals

  • The residuals are the differences between the actual data and the model predictions

  • Smaller residuals mean better fit, larger residuals mean worse fit

Ordinary least squares regression

  • We use the method of least squares to estimate the regression coefficients

  • The regression coefficients are estimates of the population parameters

  • We use \(\hat{b}_0\) and \(\hat{b}_1\) to denote the estimated coefficients

  • Ordinary least squares (OLS) regression is the most common way to estimate a linear regression model

How to find the estimated coefficients

  • There are formulas to calculate \(\hat{b}_0\) and \(\hat{b}_1\) from the data

  • The formulas involve some algebra and calculus that are not essential to understand the logic of regression

  • We can use jamovi to do all the calculations for us

  • jamovi will also provide other useful information about the regression model

Linear Regression in jamovi

  • We can use jamovi to estimate a linear regression model from the data
  • We need to specify the dependent variable and the covariate(s) in the analysis
  • jamovi will output the estimated coefficients and other statistics

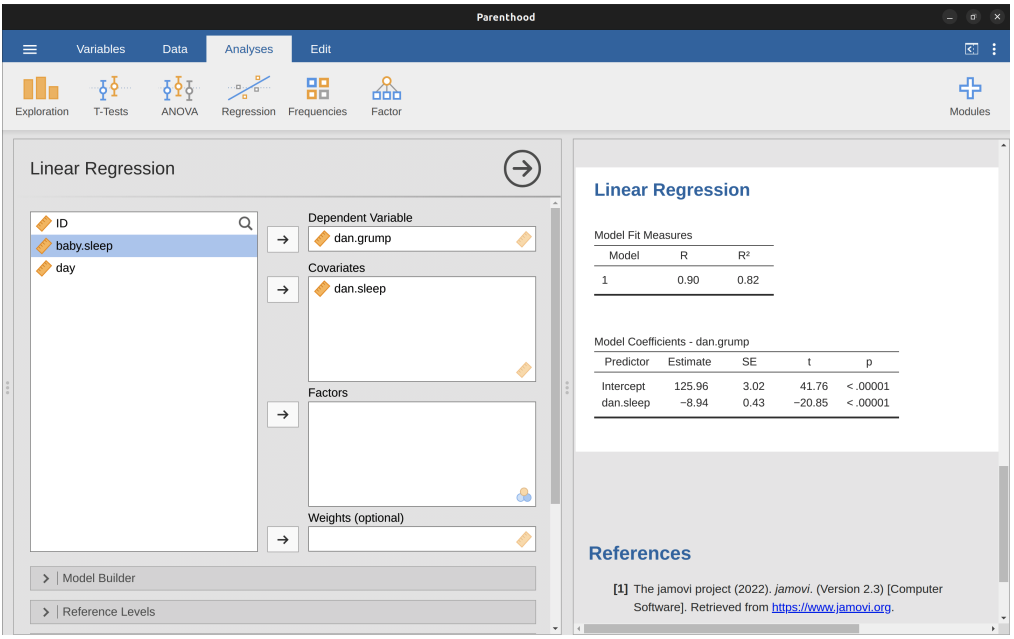
Example: Parenthood data

Data file: parenthood.csv (found in module lsj data in jamovi)

Dependent variable: dani.grump (Dani’s grumpiness)

Covariate: dani.sleep (Dani’s hours of sleep)

Estimated intercept: \(\hat{b}_0\) = 125.96

Estimated slope: \(\hat{b}_1\) = -8.94

Regression equation: \(\hat{Y}_i = 125.96+(-8.94 X_i)\)

Interpreting the estimated model

  • We need to understand what the estimated coefficients mean
  • The slope \(\hat{b}_1\) tells us how much the dependent variable changes when the covariate increases by one unit
  • The intercept \(\hat{b}_0\) tells us what the expected value of the dependent variable is when the covariate is zero

Example: Parenthood data

  • Dependent variable: dani.grump (Dani’s grumpiness)
  • Covariate: dani.sleep (Dani’s hours of sleep)
  • Estimated slope: \(\hat{b}_1\) = -8.94
    • Interpretation: Each additional hour of sleep reduces grumpiness by 8.94 points
  • Estimated intercept: \(\hat{b}_0\) = 125.96
    • Interpretation: If Dani gets zero hours of sleep, her grumpiness will be 125.96 points

Multiple Regression

Introduction

  • We can use more than one predictor variable to explain the variation in the outcome variable

    • Add more terms to our regression equation to represent each predictor variable

  • Each term has a coefficient that indicates how much the outcome variable changes when that predictor variable increases by one unit

Example: Parenthood data

  • Outcome variable: dani.grump (Dani’s grumpiness)

  • Predictor variables: dani.sleep (Dani’s hours of sleep) and baby.sleep (Baby’s hours of sleep)

Regression equation: \(Y_i=b_0+b_1X_{i1}+b_2X_{i2}+\epsilon_i\)

\(Y_i\): Dani’s grumpiness on day \(i\)

\(X_{i1}\): Dani’s hours of sleep on day \(i\)

\(X_{i2}\): Baby’s hours of sleep on day \(i\)

\(b_0\): Intercept

\(b_1\): Coefficient for Dani’s sleep

\(b_2\): Coefficient for Baby’s sleep

\(\epsilon_i\): Error term on day \(i\)

Estimating the coefficients in multiple regression

  • We want to find the coefficients that minimize the sum of squared residuals
  • Residuals are the differences between the observed and predicted values of the outcome variable
  • We use a similar method as in simple regression, but with more terms in the equation

Doing it in jamovi

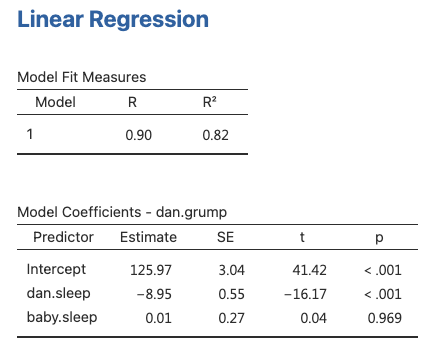
  • jamovi can estimate multiple regression models easily
  • We just need to add more variables to the Covariates box in the analysis
  • jamovi will output the estimated coefficients and other statistics for each predictor variable
  • The Table shows the coefficients for dani.sleep and baby.sleep as predictors of dani.grump

Interpreting the coefficients in multiple regression

  • The coefficients tell us how much the outcome variable changes when one predictor variable increases by one unit, holding the other predictor variables constant
  • The larger the absolute value of the coefficient, the stronger the effect of that predictor variable on the outcome variable
  • The sign of the coefficient indicates whether the effect is positive or negative

Example: Parenthood data

  • Coefficient (slope) for dani.sleep: -8.94

    • Interpretation: Each additional hour of sleep reduces Dani’s grumpiness by 8.94 points, regardless of how much sleep the baby gets

  • Coefficient (slope) for baby.sleep: 0.01

    • Interpretation: Each additional hour of sleep for the baby increases Dani’s grumpiness by 0.01 points, regardless of how much sleep Dani gets

Quantifying the fit of the regression model

  • We want to know how well our regression model predicts the outcome variable

  • We can compare the predicted values ( \(\hat{Y}_i\) ) to the observed values ( \(Y_i\) ) using two sums of squares

    • Residual sum of squares ( \(SS_{res}\) ): measures how much error there is in our predictions

    • Total sum of squares ( \(SS_{tot}\) ): measures how much variability there is in the outcome variable

The \(R^2\) value (effect size)

  • The \(R^2\) value is a proportion that tells us how much of the variability in the outcome variable is explained by our regression model

  • It is calculated as:

\[R^2=1-\frac{SS_{res}}{SS_{tot}}\]

  • It ranges from 0 to 1, with higher values indicating better fit

  • It can be interpreted as the percentage of variance explained by our regression model

The relationship between regression and correlation

  • Regression and correlation are both ways of measuring the strength and direction of a linear relationship between two variables

  • For a simple regression model with one predictor variable, the \(R^2\) value is equal to the square of the Pearson correlation coefficient (\(r^2\))

    • Running a Pearson correlation is equivalent to running a simple linear regression model

The adjusted \(R^2\) value

  • The adjusted \(R^2\) value is a modified version of the \(R^2\) value that takes into account the number of predictors in the model
    • The adjusted \(R^2\) value adjusts for the degrees of freedom in the model
  • It increases only if adding a predictor improves the model more than expected by chance

Which one to report: \(R^2\) or adjusted \(R^2\)?

  • There is no definitive answer to this question
  • It depends on your preference and your research question
  • Some factors to consider are:

    • Interpretability: \(R^2\) is easier to understand and explain

    • Bias correction: Adjusted \(R^2\) is less likely to overestimate the model performance

    • Hypothesis testing: There are other ways to test if adding a predictor improves the model significantly

Hypothesis tests for regression models

  • We can use hypothesis tests to evaluate the significance of our regression model and its coefficients
  • There are two types of hypothesis tests for regression models:

    • Testing the model as a whole: Is there any relationship between the predictors and the outcome?

    • Testing a specific coefficient: Is a particular predictor significantly related to the outcome?

Test the model as a whole

\(H_0\): there is no relationship between the predictors and the outcome

\(H_a\): data follow the regression model

\[F=\frac{(R^2/K)}{(1-R^2)/(N-K-1)}\]

  • where \(R^2\) is the proportion of variance explained by our model, \(K\) is the number of predictors, and \(N\) is the number of observations
  • The F-test statistic follows an F-distribution with \(K\) and \(N-K-1\) degrees of freedom
  • We can use a p-value to determine if our F-test statistic is significant
  • jamovi can do this for us!

Tests for Individual Coefficients

  • The F-test checks if the model as a whole is performing better than chance

  • If the F-test is not significant, then the regression model may not be good

  • However, passing the F-test does not imply that the model is good

Example of Multiple Linear Regression

  • In a multiple linear regression model with baby.sleep and dani.sleep as predictors:

    • The estimated regression coefficient for baby.sleep is small (0.01) compared to dani.sleep (-.8.95)

    • This suggests that only dani.sleep matters in predicting grumpiness

Hypothesis Testing for Regression Coefficients

  • A t-test can be used to test if a regression coefficient is significantly different from zero

\(H_0\): b = 0 (the true regression coefficient is zero)

\(H_0\): b ≠ 0 (the true regression coefficient is not zero)

Running Hypothesis Tests in Jamovi

  • To compute statistics, check relevant options and run regression in jamovi

  • See result in the next slide

Output

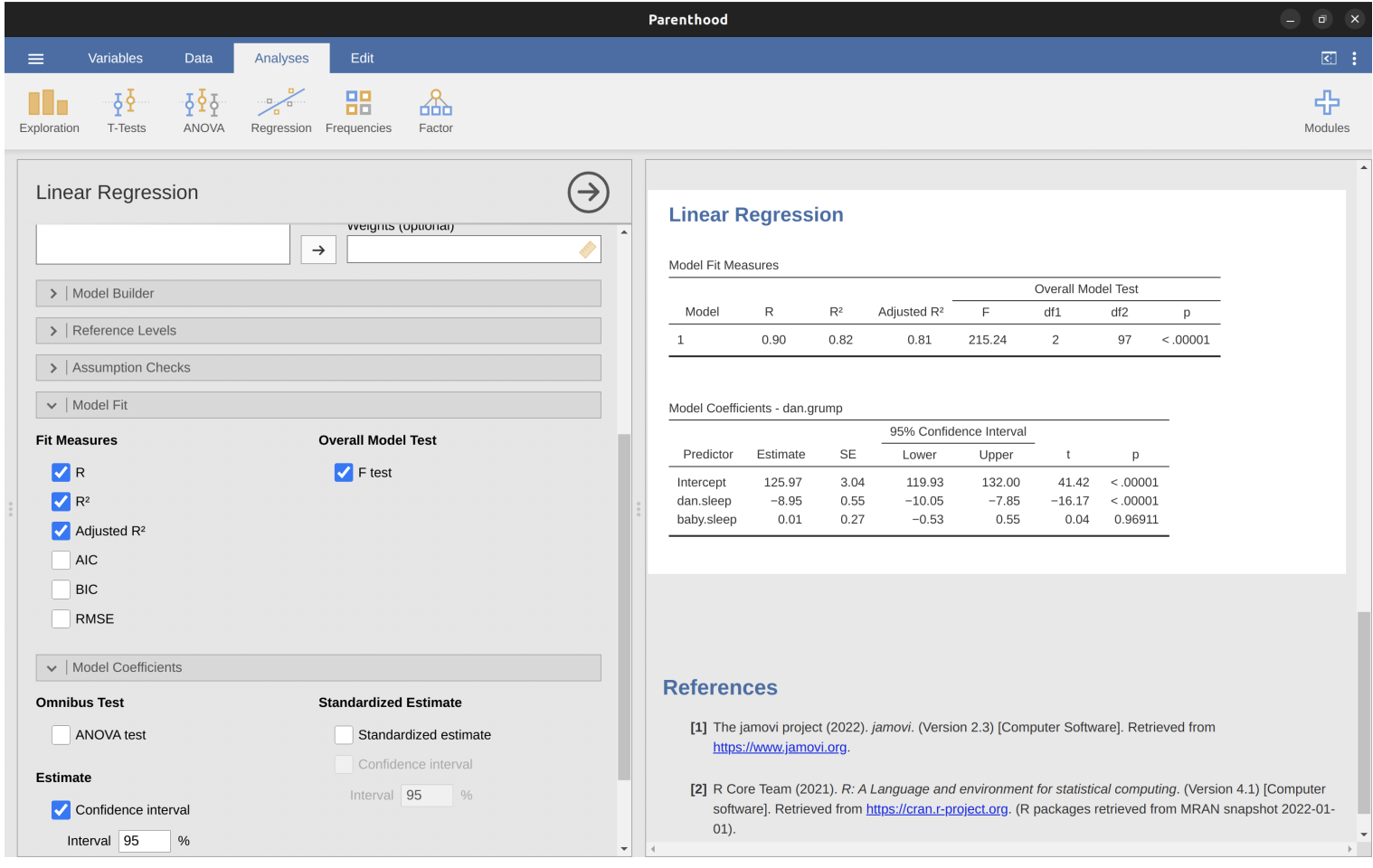
Interpretation

Conclusion

  • The current regression model may not be the best fit for the data
  • Dropping baby.sleep predictor entirely may improve the model
  • The model performs significantly better than chance

    • \(F(2,97) = 215.24\), \(p< .001\)

    • \(R^2 = .81\) value indicates that the regression model accounts for 81% of the variability in the outcome measure

  • Individual Coefficients

    • baby.sleep variable has no significant effect

    • All work in this model is being done by the dani.sleep variable

Assumptions of Regression

The linear regression model relies on several assumptions.

  • Linearity: The relationship between X and Y is assumed to be linear.

  • Independence: Residuals are assumed to be independent of each other.

  • Normality: The residuals are assumed to be normally distributed.

  • Equality of Variance: The standard deviation of the residual is assumed to be the same for all values of Y-hat.

Assumptions of Regression, cont.

Also…

  • Uncorrelated Predictors: In a multiple regression model, predictors should not be too strongly correlated with each other.

    • Strongly correlated predictors (collinearity) can cause problems when evaluating the model.

  • No “Bad” Outliers: The regression model should not be too strongly influenced by one or two anomalous data points.

    • Anomalous data points can raise questions about the adequacy of the model and trustworthiness of data.

Diagnostics

Checking for linearity

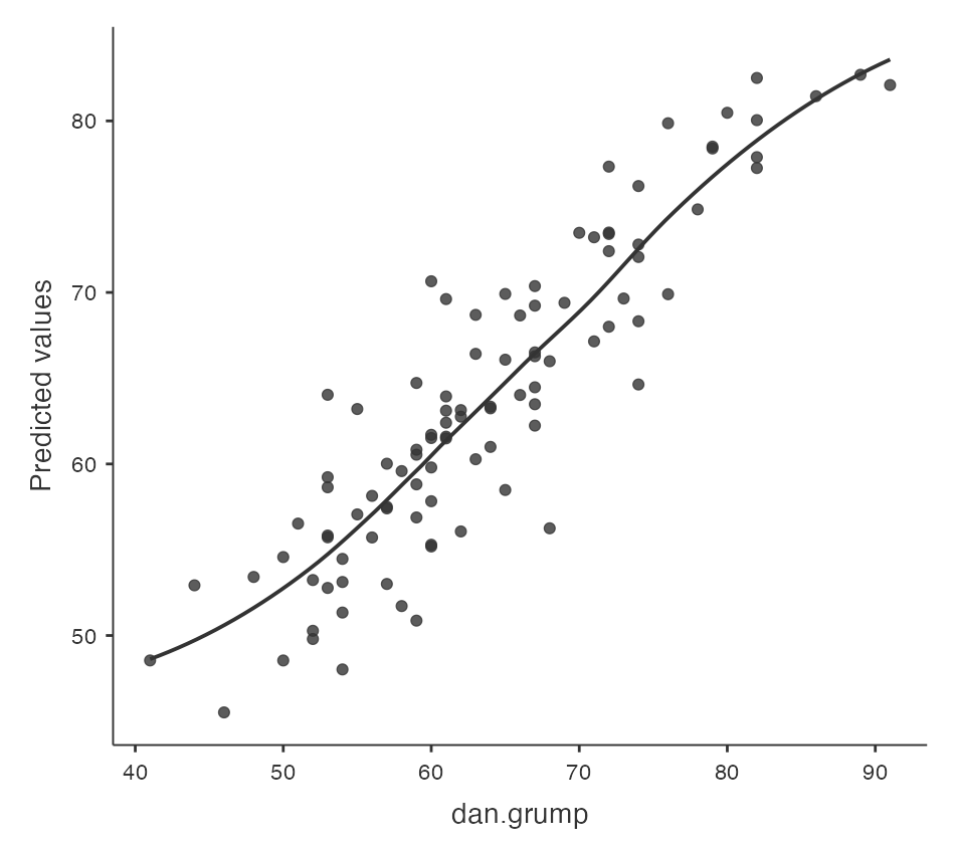
Checking Linearity

  • It is important to check for the linearity of relationships between predictors and outcomes.

Plotting Relationships

  • One way to check for linearity is to plot the relationship between predicted values and observed values for the outcome variable.

Using Jamovi

  • In Jamovi, you can save predicted values to the dataset and then draw a scatterplot of observed against predicted (fitted) values.

Interpreting Results

  • If the plot looks approximately linear, then it suggests that your model is not doing too badly. However, if there are big departures from linearity, it suggests that changes need to be made.

Checking for linearity, cont.

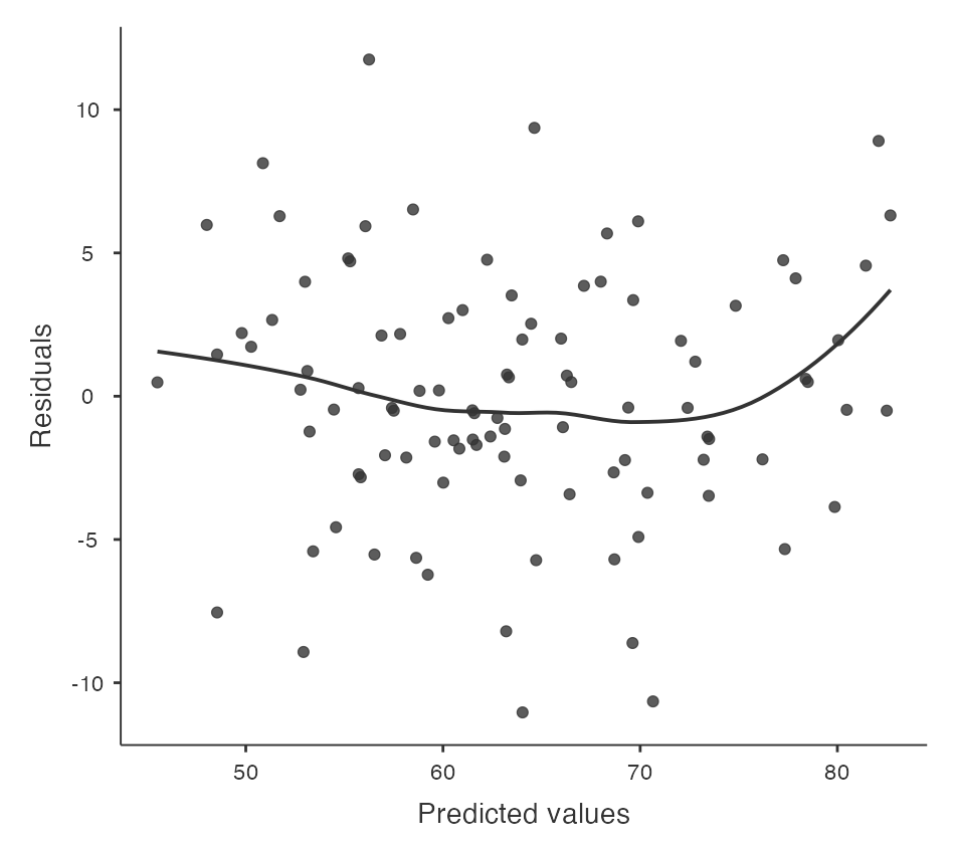
To get a more detailed picture of linearity, it can be helpful to look at the relationship between predicted values and residuals.

Using Jamovi

  • In Jamovi, you can save residuals to the dataset and then draw a scatterplot of predicted values against residual values.

Interpreting Results

  • Ideally, the relationship between predicted values and residuals should be a straight, perfectly horizontal line. In practice, we’re looking for a reasonably straight or flat line. This is a matter of judgement.

Checking for normality (residuals)

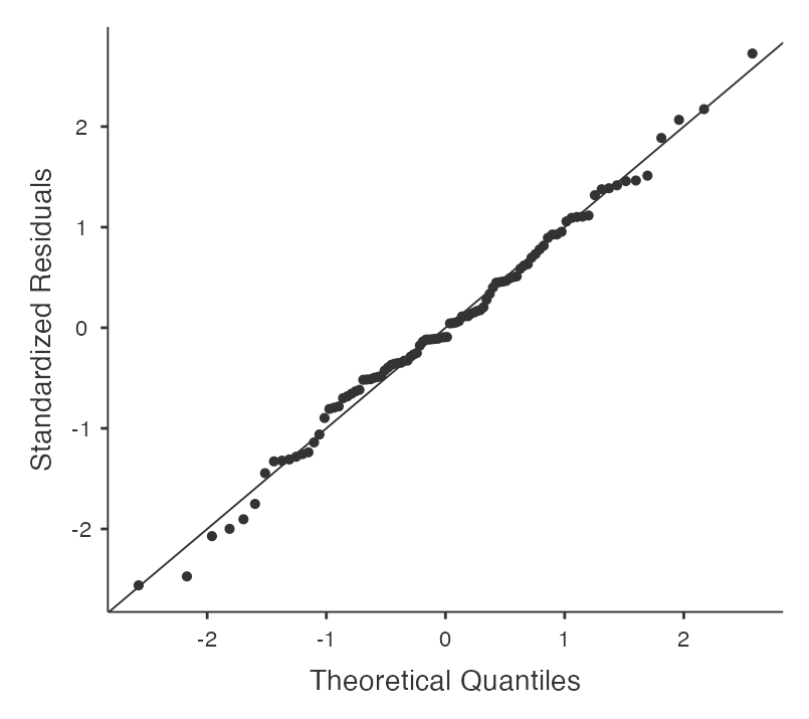
Regression models rely on a normality assumption: the residuals should be normally distributed.

Using Jamovi

  • In Jamovi, you can draw a QQ-plot via the ‘Assumption Checks’ - ‘Assumption Checks’ - ‘Q-Q plot of residuals’ option.

Interpreting Results

  • The output shows the standardized residuals plotted as a function of their theoretical quantiles according to the regression model. The dots should be somewhat near the line.

Checking for normality (residuals), cont.

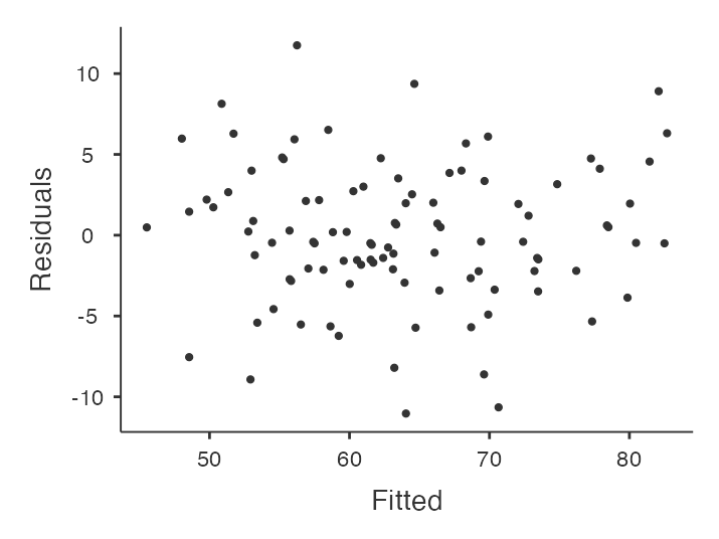
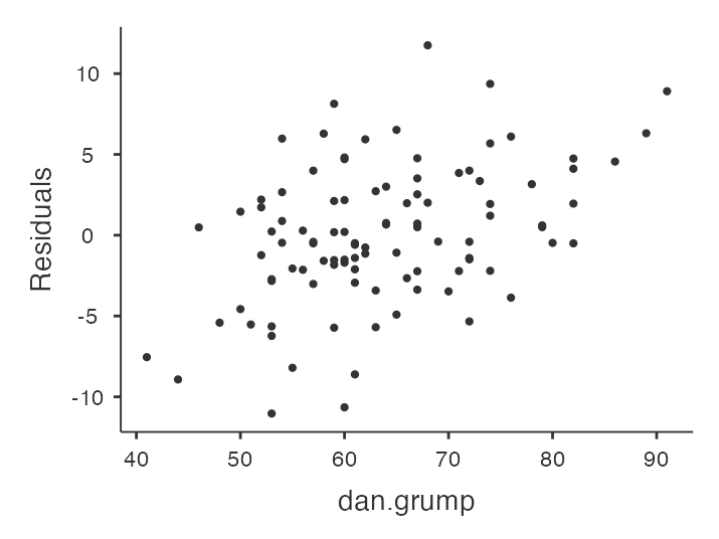
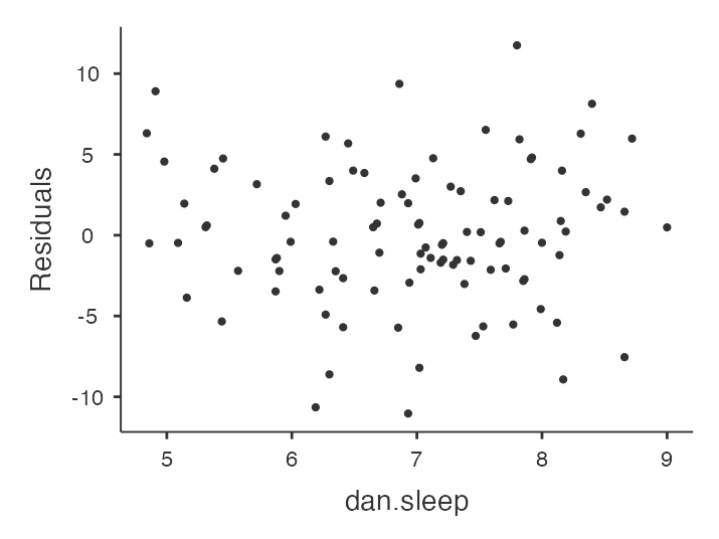
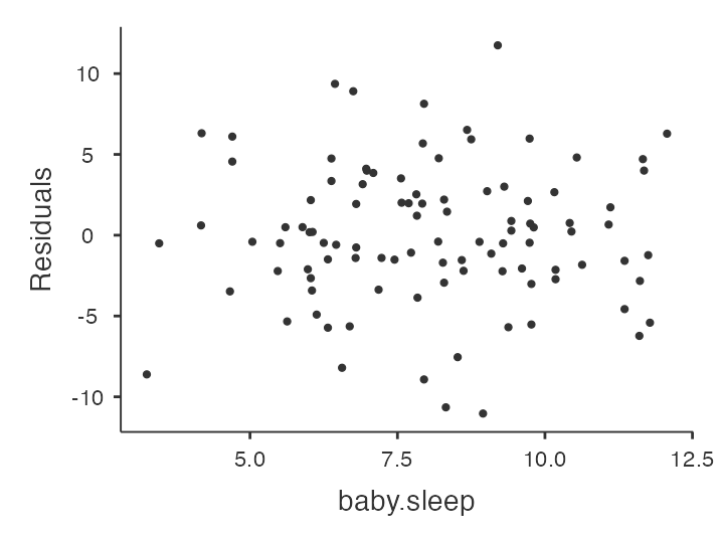
Checking Relationship between Predicted Values and Residuals

  • In Jamovi, you can use the ‘Residuals Plots’ option to check the relationship between predicted values and residuals.
  • The output provides a scatterplot for each predictor variable, the outcome variable, and the predicted values against residuals.

Interpreting Results

  • We are looking for a fairly uniform distribution of dots with no clear bunching or patterning.

    • The dots are fairly evenly spread across the whole plot

    Issues with the relationship between predicted values and residuals?

    • Transform one or more of the variables (Box-Cox Transform in jamovi)

Checking for equality of variance

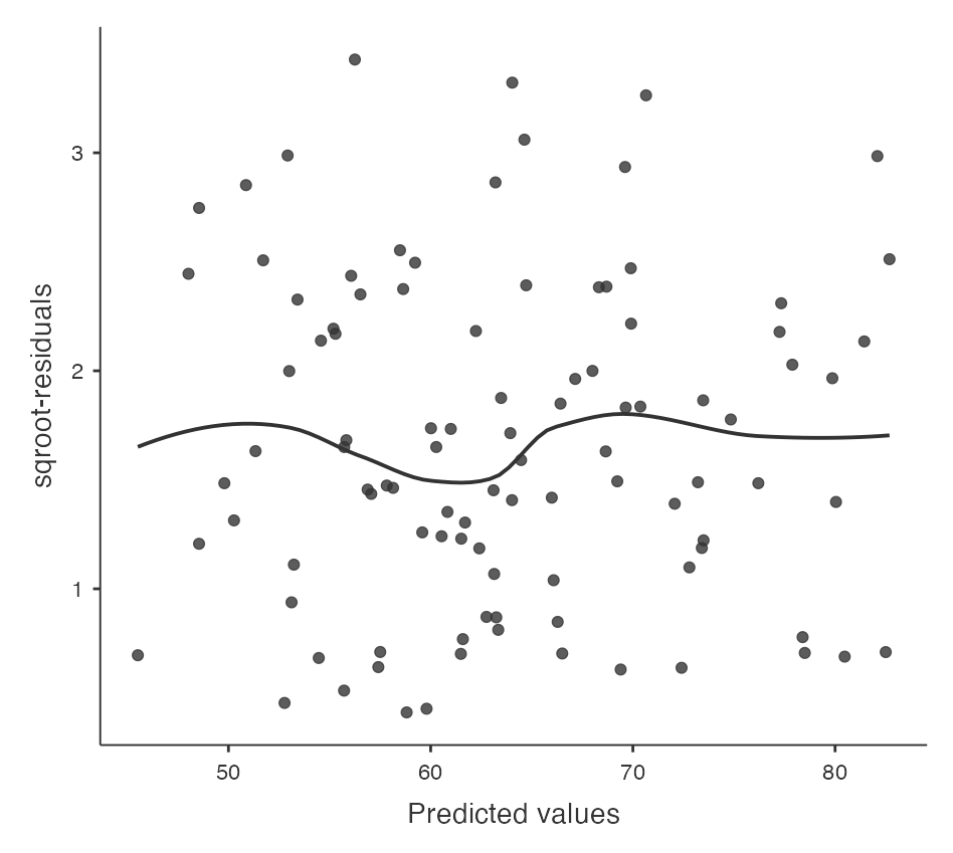
Regression models make an assumption of equality (homogeneity) of variance.

  • This means that the variance of the residuals is assumed to be constant.

Plotting Equality of Variance in Jamovi

  • To check this assumption in Jamovi, first calculate the square root of the absolute size of the residual.
    • Compute this new variable using the formula SQRT(ABS(Residuals))
  • Then plot this against the predicted values.
  • The plot should show a straight horizontal line running through the middle.

Checking for Collineary

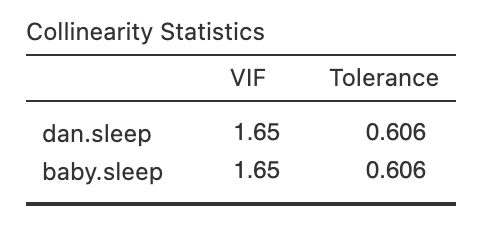
  • Variance Inflation Factors (VIFs) can be used to determine if predictors in a regression model are too highly correlated with each other.
    • Each predictor has an associated VIF.
  • In Jamovi, click on the ‘Collinearity’ checkbox in the ‘Regression’ - ‘Assumptions’ options to see VIF values.
  • Interpreting VIF
    • A VIF of 1 means no correlation among the predictor and the remaining predictor variables
    • VIFs exceeding 4 warrant further investigation
    • VIFs exceeding 10 are signs of serious multicollinearity requiring correction

Checking for outliers

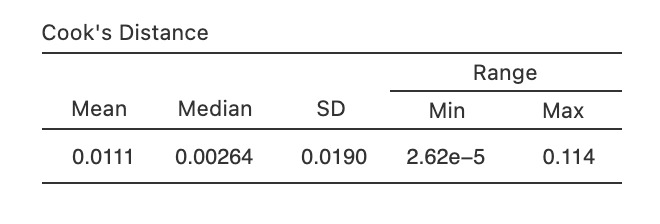
  • Used in regression analysis to identify influential data points that may negatively affect your regression model
  • Datasets with a large number of highly influential points might not be suitable for linear regression without further processing such as outlier removal or imputation
  • Identifying Outliers
    • A general rule of thumb: Cook’s distance greater than 1 is often considered large
  • What if the value is greater than 1?

    • remove the outlier and run the regression again

    • How? In jamovi you can save the Cook’s distance values to the dataset, then draw a boxplot of the Cook’s distance values to identify the specific outliers.

References

https://drfurtado.github.io/kin610/

Navarro, Danielle J, and David R Foxcroft. 2022. Learning Statistics with Jamovi: A Tutorial for Psychology Students and Other Beginners (Version 0.75). Danielle J. Navarro; David R. Foxcroft. https://doi.org/10.24384/HGC3-7P15.