Week 3 (Ch05)

Motor Control Theories

Ovande Furtado Jr., PhD.

Associate Professor, California State University, Northridge

2025-10-05

Presentation Viewing Recommendations

• This presentation is better viewed in a web browser, either on a computer or tablet. I do not recommend using mobile phones.
• Use keyboard shortcuts for navigation (e.g., arrow keys, spacebar).
• Use keyboard key “A” to pause/play audio on the current slide.
• The audio will automatically pause when you navigate to a different slide.
• Use keyboard key “S” for different viewing modes.
• If you issues with audio playback and captions, try a different web browser (e.g., Chrome, Firefox, Safari).

The PDF version of this presentation can be downloaded from the Download link at the top.

Objectives

1. Discuss the relevance of motor control theory for the practitioner
2. Define the term coordination
3. Describe the degrees of freedom problem
4. Compare and contrast an open-loop control system and a closed-loop control system
5. Describe a primary difference between a motor program–based theory and a dynamical systems theory of motor control

6. Define a generalized motor program and describe an invariant feature and a parameter proposed to characterize this program
7. Define the following terms associated with dynamical systems theory: order and control parameters, self-organization, coordinative structures, perception-action coupling, affordances
8. Discuss how a motor program–based theory and a dynamical systems theory each explain the relative-time characteristics of human walking and running

Welcome to our exploration of motor control theories, one of the most fascinating areas in the study of human movement. Today we’re going to dive into Chapter 5, where we’ll discover how different theories explain the amazing ability we have to control our coordinated movements. Think about something as simple as reaching for your coffee cup this morning - behind that seemingly effortless action lies an incredibly complex control system that scientists have been trying to understand for decades. What’s particularly interesting is that theories about motor control differ significantly in how they explain this process. Some theories emphasize the role of our central nervous system, almost like a computer program running the show, while others focus more on how we interact dynamically with our environment. By the end of today’s session, you’ll understand these competing perspectives and appreciate why this debate matters so much for professionals working in fields like physical therapy, athletic training, and sports coaching. We’ll explore eight key learning objectives that will give you a solid foundation in motor control theory, from basic concepts like coordination and degrees of freedom, all the way to complex theoretical frameworks that shape how we understand human movement.

1 Concept

• Theories about how we control coordinated movement differ in terms of the roles of central and environmental features of a control system

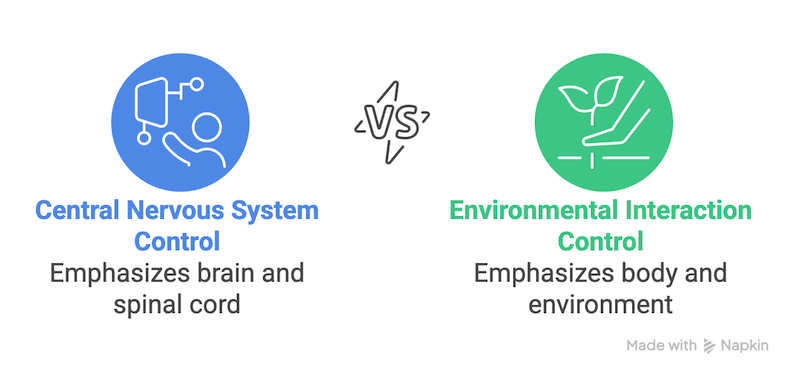
Fig. 1.0: Theories about how we control coordinated movement differ in terms of the roles of central and environmental features of a control system.

Let’s start with a fundamental concept that lies at the heart of motor control theory. The central idea we need to grasp is that theories about how we control coordinated movement differ significantly in terms of the roles they assign to central features versus environmental features of a control system. Now, what do I mean by this? When we talk about central features, we’re referring to things happening inside your nervous system - your brain, spinal cord, and the neural pathways that process and send movement commands. Think of this as the “internal computer” approach to understanding movement control. On the other hand, environmental features refer to all the external factors around us - the surface we’re walking on, the weight of an object we’re lifting, the wind affecting a ball we’re trying to catch. Some theories heavily emphasize these central, internal mechanisms, suggesting that our nervous system contains pre-programmed instructions for movement, much like software running on a computer. Other theories argue that movement emerges more from our dynamic interaction with the environment, where the external world plays a much larger role in shaping how we move. This fundamental difference in perspective creates a fascinating debate in motor control research, and understanding this distinction will help you appreciate why different theories lead to different approaches in teaching motor skills and treating movement disorders.

2 Actions are Continuously Adapted to the Environment

• Movement behavior is constantly adjusted based on environmental demands
• Real-time adaptation is essential for successful motor performance

Fig. 2.0: A dynamic scene of a soccer player dribbling through cones, with multiple exposure/motion blur effects showing how the player’s movements adapt and change in real-time to navigate around obstacles, emphasizing the continuous nature of motor adaptation.

Here’s something truly remarkable about human movement that often goes unnoticed - our actions are continuously adapted to the environment in real-time. Picture yourself walking down a busy sidewalk. You’re not just following a pre-set program for walking; instead, you’re constantly adjusting your steps to avoid other pedestrians, stepping around puddles, and modifying your pace based on the crowd. This image perfectly illustrates the dynamic nature of motor control. Your nervous system is constantly receiving information from your environment - visual cues about obstacles ahead, proprioceptive feedback about the ground surface, auditory information about approaching traffic. What’s fascinating is how seamlessly these environmental adaptations occur without conscious thought. When you encounter an unexpected crack in the sidewalk, you don’t stop to consciously plan how to step over it; your movement system automatically adjusts. This continuous adaptation challenges theories that suggest movements are entirely pre-programmed. Instead, it supports the idea that successful motor control requires ongoing interaction between the performer and their environment. This concept becomes especially important when we consider how athletes perform in unpredictable conditions or how patients recovering from injury must relearn to move in their changing physical capabilities. Understanding this adaptive nature of movement helps explain why some motor control theories emphasize environmental information as a crucial component of the control process.

3 What is a Theory?

• Accurately describes a large class of observations
• Makes definite predictions about results of future observations (Hawking, 1996)
• Motor learning and control theories focus on:
  • Explaining human movement behavior
  • Providing explanations about why people perform skills as they do

Fig. 3.0: A scientist or researcher observing and documenting human movement patterns, with visual elements showing the progression from observation to theory development - perhaps showing movement patterns being analyzed and converted into theoretical models and predictions.

Before we dive deeper into motor control theories, we need to establish what we mean by “theory” in a scientific context. You might think of theory as just speculation or guesswork, but in science, a theory is much more powerful and precise than that. According to renowned physicist Stephen Hawking, a good scientific theory must satisfy two critical requirements. First, it must accurately describe a large class of observations - meaning it can explain many different phenomena, not just isolated cases. Second, it must make definite predictions about the results of future observations, allowing scientists to test its validity. In the context of motor learning and control, theories serve a specific purpose: they focus on explaining human movement behavior and providing explanations about why people perform skills as they do. Think about a physical therapist working with a stroke patient who has difficulty walking. A good motor control theory helps explain why certain movement patterns are impaired and predicts which interventions might be most effective. Or consider a tennis coach trying to help a player improve their serve. Theory provides the framework for understanding why certain techniques work better than others and how practice should be structured. This scientific approach to understanding movement is what separates evidence-based practice from simple trial and error. When we understand the underlying theories, we can make informed decisions about how to teach skills, design rehabilitation programs, and optimize athletic performance.

4 How Does Theory Relate to Professional Practice?

• Provides the “why” basis for what practitioners do
• Bridges the gap between scientific understanding and practical application

Fig. 4.0: A diagram illustrating the relationship between theory and practice in motor control, with arrows showing the flow of information and feedback between research and application.

Now you might be wondering, “Why do I need to understand theory when I just want to help people move better?” This is a great question that many students ask, and the answer is fundamental to becoming an effective practitioner. Theory provides the essential “why” basis for what practitioners do in their daily work. Without theoretical understanding, practice becomes merely a collection of techniques without deeper comprehension. Imagine you’re a physical therapist and a patient asks why you’re having them practice reaching movements in different directions. With theoretical knowledge, you can explain that motor control theory suggests the nervous system organizes movements in flexible patterns that can adapt to various conditions, so practicing in multiple contexts helps rebuild these adaptive capabilities. This theoretical foundation also bridges the gap between scientific understanding and practical application. When you understand the principles behind movement control, you can adapt your interventions to meet individual needs rather than simply following cookbook approaches. Theory guides evidence-based practice by helping practitioners understand the mechanisms behind movement, which improves intervention and training strategies. It also enables better prediction of outcomes - if you understand how the motor control system responds to different types of practice, you can design more effective training programs. Perhaps most importantly, when your initial approach isn’t working, theoretical knowledge provides the foundation for creating alternative instruction and practice conditions. This flexibility and adaptability, grounded in solid theoretical understanding, is what separates expert practitioners from those who simply follow procedures.

5 Relevance of Theory for Practitioners

• Theory guides evidence-based practice
• Helps practitioners understand the mechanisms behind movement
• Improves intervention and training strategies
• Enables better prediction of outcomes

Fig. 5.0: A visual representation of the relevance of theory for practitioners in motor control, showing the connections between theory, practice, and outcomes.

Chart adapted from Magill & Anderson (2017)

Let’s explore more deeply how motor control theory empowers practitioners across different fields. The relevance of theory extends far beyond academic understanding - it provides a comprehensive foundation that supports virtually every aspect of professional practice. When you understand motor control theory, you gain the ability to understand and explain motor skill performance constraints, limits, potential, and deficits. This means you can look at a patient’s movement difficulties or an athlete’s performance limitations and understand the underlying mechanisms at work. Theory also enables you to identify performance problems more accurately. Instead of just seeing that someone moves awkwardly, you can pinpoint whether the issue stems from coordination difficulties, problems with environmental adaptation, or challenges with motor program execution. This diagnostic capability leads to more targeted interventions. Furthermore, theoretical knowledge allows you to predict the effectiveness of intervention strategies before implementing them. If you understand how the motor control system responds to different types of practice or therapy, you can choose approaches that are more likely to succeed. When standard interventions aren’t working, theory provides the foundation for developing creative, alternative strategies. This is particularly valuable in rehabilitation settings where patients may have unique combinations of impairments requiring individualized approaches. Finally, theory enables you to evaluate the effectiveness of your interventions systematically, helping you refine your practice over time. All of these capabilities contribute to developing a systematic approach that helps individuals increase their skill performance capabilities, whether they’re athletes seeking peak performance or patients recovering from injury.

6 Motor Control Theory

• Describes and explains how the nervous system produces coordinated movement during motor skill performance in a variety of environments
• Two important terms:
  • Coordination
  • The degrees of freedom problem

Fig. 6.0: Illustrate the nervous system (brain, spinal cord, and peripheral nerves) controlling a complex movement like throwing a ball, with highlighted pathways showing neural control and coordination of multiple body segments working together.

Now that we understand why theory matters, let’s dive into what motor control theory actually addresses. Motor control theory describes and explains how the nervous system produces coordinated movement during motor skill performance in a variety of environments. This is quite a comprehensive task when you think about it. Consider how your nervous system manages to coordinate the hundreds of muscles and numerous joints involved in something as complex as a tennis serve, and does so consistently whether you’re playing on a clay court in humid conditions or a hard court on a windy day. To understand this remarkable capability, motor control theory focuses on two particularly important concepts that we’ll be exploring in detail. The first is coordination - the fundamental organizational principle that allows all those muscles and joints to work together effectively rather than fighting against each other. Think of coordination as the conductor of an orchestra, ensuring that all the different instruments (in this case, muscles and joints) contribute harmoniously to create beautiful music (smooth, effective movement). The second crucial concept is the degrees of freedom problem, which addresses one of the most challenging questions in motor control: how does the nervous system manage to control the enormous number of independent moving parts in the human body to produce specific, intended actions? These two concepts form the foundation for understanding how we accomplish the seemingly impossible task of moving skillfully and adaptively in our complex, ever-changing world.

7 Coordination Definition

• Patterning of body and limb motions relative to the patterning of environmental objects and events (Turvey, 1990)
• Two parts to consider:
  • Relations among joints and body segments at a specific point of time
  • Relation between pattern of coordination and the environment so the action can be accomplished

Fig. 7.0: A diagram illustrating the relationship between coordination and the environment in motor control, highlighting the interactions between body movements and external factors.

Let’s establish a clear understanding of what coordination means in the context of motor skill performance. According to researcher Michael Turvey, coordination is the patterning of head, body, and limb movements relative to the patterning of environmental objects and events. This definition contains two essential components that we need to unpack. First, coordination involves patterns of head, body, and limb movements. This means we’re not just looking at individual muscles or joints working in isolation, but rather how they work together as an integrated system. When you watch a skilled basketball player shooting a free throw, you’re observing a coordinated pattern where the legs provide a stable base, the torso rotates appropriately, the arm extends in a smooth arc, and the wrist snaps at just the right moment. Each part contributes to the whole movement pattern. The second part of Turvey’s definition emphasizes that these movement patterns occur relative to environmental objects and events. This is crucial because it recognizes that coordination isn’t just about internal organization - it’s about organizing movement in relation to what’s happening around us. A soccer player doesn’t just kick the ball with a predetermined pattern; they coordinate their kicking movement relative to the ball’s position, the goal location, the defender’s approach, and the field conditions. This environmental component means that effective coordination requires both internal organization among body parts and appropriate adaptation to external circumstances. Understanding coordination this way helps explain why movement looks different in different situations, even when the basic skill remains the same.

8 Coordination in a Soccer Kick

• Angle-Angle Diagram (Anderson & Sidaway, 1994)
• Demonstrates the coordinated relationship between joints during movement
• Shows how different joints work together in a coordinated pattern

Fig. 8.0: Angle-angle diagram showing the coordinated relationship between hip and knee angles during a soccer kick, demonstrating the cyclical pattern and timing of joint movements.

Image credit: Magill & Anderson (2017)

To better understand coordination in action, let’s examine a specific example: the coordination patterns observed in a soccer kick. The research by Anderson and Sidaway provides us with a fascinating visualization called an angle-angle diagram that reveals the coordinated relationship between joints during movement. In this particular study, researchers tracked the hip and knee angles throughout the soccer kicking motion and plotted one against the other. What emerges is a beautiful pattern that shows how these two joints work together in a coordinated fashion. The angle-angle diagram demonstrates that the hip and knee don’t move independently; instead, they follow a specific relationship throughout the kick. As the hip angle changes in one direction, the knee angle changes in a predictable, coordinated manner. This relationship isn’t random - it reflects the underlying coordination pattern that makes an effective soccer kick possible. What’s particularly interesting is how this diagram can reveal changes in coordination that occur with practice. Novice players might show more erratic, less coordinated patterns, while skilled players demonstrate smooth, consistent relationships between joint movements. This type of analysis helps us understand that coordination isn’t just about moving multiple body parts simultaneously; it’s about organizing those movements in specific, functional relationships. The soccer kick example illustrates how different joints must work together in a coordinated pattern, with each joint’s movement being precisely timed and scaled relative to the others to achieve the intended goal of striking the ball effectively.

9 Degrees of Freedom Problem

• Degrees of freedom (df) = Number of independent elements in a system and the ways each element can act
• Degrees of freedom problem = How to control the df to make a complex system act in a specific way
• Example: The control of a helicopter’s flight
• For movement: How does the nervous system control the many df of muscles, limbs, and joints to enable a person to perform an action as intended?

Fig. 9.0: Illustration of the degrees of freedom problem in motor control, showing the challenge of coordinating multiple independent elements (joints, muscles, limbs) to achieve a specific movement goal.

Now we come to one of the most fundamental challenges in motor control - the degrees of freedom problem. This concept was first posed by Nicolai Bernstein, a Russian physiologist whose groundbreaking work from the 1930s-1950s became influential in the Western world after 1967. Bernstein addressed a mind-boggling question: how does the nervous system control the enormous number of independent components in the human body to produce specific, coordinated movements? Let’s start by understanding what “degrees of freedom” means. In any system, degrees of freedom refer to the number of independent elements and the ways each element can act. The degrees of freedom problem, therefore, is how to control these degrees of freedom to make a complex system act in a specific way. To appreciate the magnitude of this challenge, consider that the human body has approximately 792 muscles and over 100 joints, each capable of acting in various ways. Think about your elbow joint - it has two degrees of freedom because it can flex and extend. That might seem manageable, but when we multiply this across the entire body, we’re dealing with an astronomical number of independent variables that somehow need to be coordinated to produce a single, smooth movement. A common analogy is the control of a helicopter’s flight. A helicopter has multiple independent controls that all affect its movement in different ways. The pilot must coordinate all these controls simultaneously to make the helicopter go where they want it to go. Similarly, your nervous system must coordinate hundreds of muscles and joints to produce coordinated movement. To put this in perspective, consider something as seemingly simple as picking up a drinking glass. Using just one hand, you need to control at least 18 joints - the shoulder, elbow, wrist, and 15 finger and thumb joints. The challenge for your nervous system is enormous: how do you coordinate all these independent moving parts to produce the precise, smooth reaching and grasping movement needed to successfully pick up the glass without dropping it or crushing it?

10 Bernstein’s Classic Demonstration

• Nicolai Bernstein demonstrated the degrees of freedom problem with an experiment (originally published in Russian in 1957)
• A subject fastens a ski-stick to their belt with a weight at the far end
• Rubber tubing is attached to the stick’s end, and the subject holds the ends of the tubing in their hands
• The task: Try to follow the contours of a figure drawn on a vertical board with the point of the ski-stick, manipulating it only by pulling the rubber tubing
• The ski-stick represents one limb segment with two degrees of freedom, and the tubing acts as two antagonistic muscles, adding two more degrees of freedom, totaling four degrees of freedom in the system
• This experiment clearly shows how difficult and complicated it is to control systems requiring the coordination of even four degrees of freedom without prior motor practice

Fig. 10.0: Bernstein’s demonstration of the degrees of freedom problem showing three stages of learning the overarm throw. Stage 1: Freezing degrees of freedom with restricted arm movement. Stage 2: Releasing degrees of freedom with more leg and trunk movement. Stage 3: Exploiting degrees of freedom by taking advantage of reactive forces and passive dynamics.

Image credit: Haywood & Getchell (2024)

To help you truly understand the complexity of the degrees of freedom problem, let me describe a famous demonstration that Nicolai Bernstein conducted in 1957. This classic experiment vividly illustrates just how difficult it is to control even a relatively simple system with multiple degrees of freedom. In Bernstein’s demonstration, a subject fastens a ski-stick to their belt with a weight at the far end to simulate a limb segment. Rubber tubing is then attached to the stick’s end, and the subject holds the ends of the tubing in their hands, essentially creating a simplified model of muscular control. The task seems straightforward: try to follow the contours of a figure drawn on a vertical board with the point of the ski-stick, manipulating it only by pulling the rubber tubing. Now, this might sound simple, but here’s where it gets interesting. The ski-stick represents one limb segment with two degrees of freedom - it can move in different directions around the attachment point. The rubber tubing acts as two antagonistic muscles, adding two more degrees of freedom to the system. So in total, this simplified system has four degrees of freedom - far fewer than the hundreds we typically deal with in normal human movement. The results of this experiment are both humbling and enlightening. Subjects find it extremely difficult and complicated to control this system requiring the coordination of even just four degrees of freedom, especially without prior motor practice. People struggle to make smooth, accurate movements, and their attempts to trace the figure are often jerky, imprecise, and require intense concentration. This demonstration beautifully illustrates the central challenge of motor control: if controlling just four degrees of freedom is this difficult, imagine the incredible computational and coordination challenge your nervous system faces every time you perform even the simplest movement with your actual body, which has hundreds of degrees of freedom. It’s a powerful reminder of just how sophisticated our motor control system really is, and why understanding how it works is such a fascinating and complex scientific challenge.

11 Two General Types of Control Systems

• Open-loop control systems
• Closed-loop control systems
• Each represents different approaches to motor control
• Both are incorporated into motor control theories

Fig. 11.0: Open-loop and closed-loop motor control systems.

Now that we understand the complexity of the degrees of freedom problem, let’s explore how motor control theories address this challenge through different control system approaches. Motor control theories incorporate two general types of control systems, each representing fundamentally different approaches to understanding how our nervous system manages coordinated movement. These two types are open-loop control systems and closed-loop control systems, and understanding their differences is crucial for grasping how different theories explain motor control. Both types of control systems are incorporated into motor control theories, but they emphasize different aspects of how movement is controlled and coordinated. The distinction between these systems helps us understand the ongoing debates in motor control research and provides a framework for thinking about when and how different control mechanisms might be employed. Open-loop control systems represent one approach where movement commands are issued without the use of feedback during execution. Think of this like a pre-programmed sequence that runs to completion once it’s started. Closed-loop control systems, on the other hand, rely heavily on feedback information to guide and modify movement as it unfolds in real time. What’s particularly important to understand is that both approaches have merit and both are likely involved in human motor control, depending on the specific demands of the task, the speed of the movement, and the environmental conditions. Rather than viewing these as mutually exclusive alternatives, modern motor control theories often consider how these different control approaches might work together or be selectively employed based on the circumstances. The beauty of having both types of control systems available is that it allows for tremendous flexibility in how we control movement. Some situations may call for rapid, ballistic movements that rely more on open-loop control, while others may require continuous adjustments based on sensory feedback, calling for closed-loop control. Understanding these distinctions will help you appreciate the complexity and elegance of human motor control.

12 Open-Loop vs Closed-Loop Control Systems

• Incorporated into all theories of motor control
• Show different ways the CNS and PNS initiate and control action
• Each has a central control center (executive)
• Function to generate and forward movement instructions to effectors (i.e., muscles)
• Content of the instructions differs between systems

Fig. 12.0: Open-loop and closed-loop motor control systems.

Now let’s examine these two control systems more closely to understand how they’re incorporated into motor control theories. Both open-loop and closed-loop control systems appear in virtually all theories of motor control because they represent fundamentally different ways that the central nervous system and peripheral nervous system can initiate and control action. Each system includes a central control center, which we can think of as the executive decision-maker. This control center has the crucial function of generating and forwarding movement instructions to the effectors - those muscles that will actually carry out the movement. Both systems involve this basic flow of information from the control center to the muscles, but here’s where the similarity ends. The critical difference lies in the content and timing of the instructions that flow between these components. In some movements, all the necessary information might be contained in the initial instructions sent from the control center, while in other movements, the initial instructions might only get the movement started, with additional guidance provided as the movement unfolds. This difference in instruction content and timing reflects two very different philosophies about how complex movements can be controlled. Understanding these differences helps explain why certain types of movements seem to fit one model better than the other, and why both models are necessary to fully account for the range of human movement capabilities we observe in daily life and sports performance.

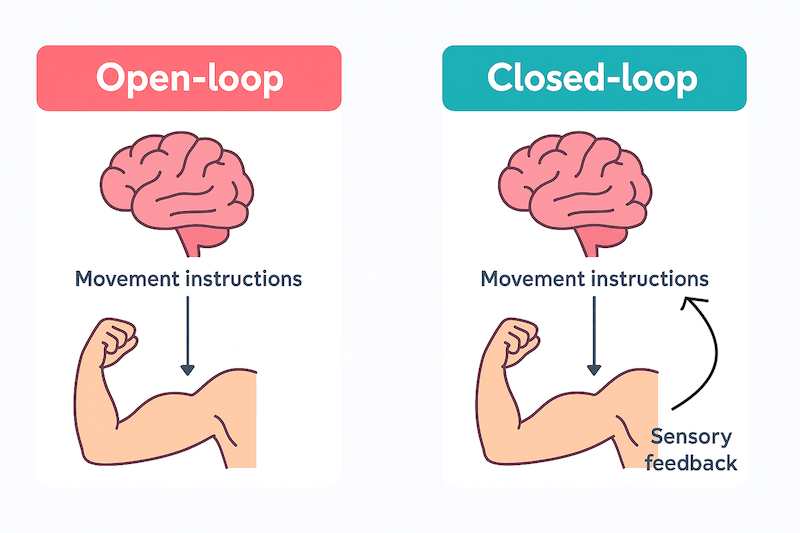
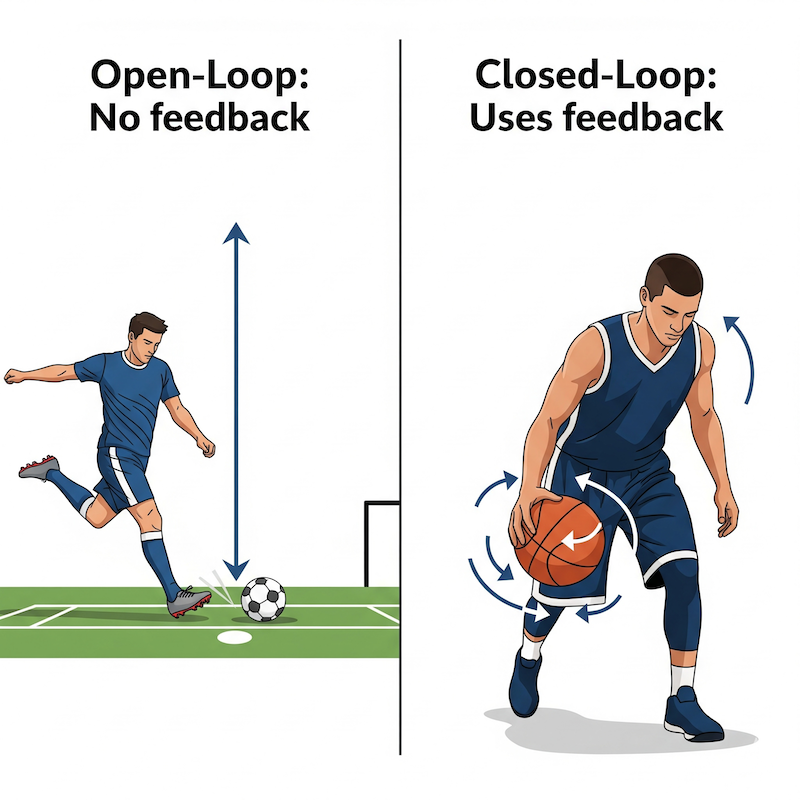
13 Differences Between the Systems

Open-Loop: - Does not use feedback - Control center provides all the information for effectors to carry out movement

Closed-Loop: - Uses feedback - Control center issues information to effectors sufficient only to initiate movement - Relies on feedback to continue and terminate movement

Fig. 13.0: A split-screen that contrasts open-loop and closed-loop sports actions. On the left, a soccer player taking a penalty kick is labeled “Open-Loop: No feedback,” showing a pre-planned swing. On the right, a basketball player dribbling while watching the ball is labeled “Closed-Loop: Uses feedback,” with arrows indicating real-time adjustments.

Let’s explore the key differences between open-loop and closed-loop control systems by examining how each handles the flow of information during movement. In an open-loop system, the most defining characteristic is that it does not use feedback to control ongoing movement. Think of this like a pre-programmed sequence - once it starts, it runs its course without modification. The control center provides all the information necessary for the effectors to carry out the planned movement within the initial instructions. It’s like giving someone extremely detailed directions to a destination, including every turn and landmark, so they can complete the entire journey without needing to call for additional guidance. A perfect mechanical example is a digital video recorder that’s programmed to record a television show. You set it to record from 8:00 to 9:00 PM, and it will do exactly that, even if the show runs over or ends early - it can’t adjust based on the actual content. In human movement, think about throwing a dart at a dartboard. Once you release the dart, the flight path is determined by the initial conditions you created - the force, angle, and spin you imparted. You can’t control the dart once it’s airborne. In contrast, a closed-loop system actively involves feedback throughout the movement. The control center issues initial instructions that are sufficient only to initiate the movement, but the actual execution and completion depend heavily on feedback information that continuously updates the control center about how the movement is progressing. This feedback allows for real-time adjustments and corrections, making the system much more adaptive but also more complex to manage.

14 Two Theories of Motor Control

• Motor Program-based theory: Memory-based mechanism that controls coordinated movement
• Dynamical Systems Theory: Emphasizes the role of information in the environment and mechanical properties of the body and limbs in movement control/coordination

Now that we understand control systems, we can explore how they relate to the two major theories that dominate our understanding of motor control. These theories represent fundamentally different perspectives on how the nervous system produces coordinated movement, and each emphasizes different aspects of the control process. The first major approach is motor program-based theory, which proposes that coordinated movement is controlled by memory-based mechanisms. Think of this as the “internal software” approach to motor control. According to this perspective, your nervous system contains stored programs - like computer software - that contain the essential instructions for classes of movements. When you want to throw a ball, for example, your nervous system retrieves and executes a throwing motor program, adjusting specific parameters like force and direction for the particular situation. This approach emphasizes central, memory-based control and tends to align more with open-loop control concepts. The second major approach is dynamical systems theory, which takes a dramatically different perspective. This theory emphasizes the role of information in the environment and the mechanical properties of the body and limbs in movement control and coordination. Rather than relying primarily on pre-stored programs, this approach suggests that coordinated movement patterns emerge from the dynamic interaction between the performer, the task demands, and the environmental constraints. This perspective aligns more closely with closed-loop control concepts and emphasizes the continuous, adaptive nature of movement control. Understanding these two theoretical frameworks will help you appreciate the ongoing debates in motor control research and their practical implications for teaching and rehabilitation.

15 Motor Program-Based Theory (Schema Theory)

• “Schema Theory” by Schmidt (1988)
• Generalized motor program (GMP): Hypothesized memory-based mechanism responsible for adaptive and flexible qualities of human movement
• Proposed that each GMP controls a class of actions, which are identified by common invariant characteristics
• GMP Function: To serve as the basis for generating movement instructions prior to and during the performance of an action

Let’s dive deeper into the first major theory of motor control: motor program-based theory, which is most comprehensively developed in what’s known as “Schema Theory” by Richard Schmidt, published in 1988. This theory represents a sophisticated attempt to explain how our nervous system can produce the remarkable flexibility and adaptability we see in human movement while still maintaining consistency and efficiency.

At the heart of this theory is the concept of the generalized motor program, or GMP, which Schmidt proposed as a hypothesized memory-based mechanism responsible for the adaptive and flexible qualities of human movement. Think of a GMP as a flexible template or blueprint stored in your nervous system that contains the essential structure for a class of related movements, rather than specific instructions for just one particular movement.

The key insight that Schmidt brought to motor program theory is that each GMP controls not just a single, specific action, but rather an entire class of actions that share common invariant characteristics. For example, rather than having separate motor programs for throwing a baseball, throwing a football, and throwing a dart, Schmidt proposed that you have one throwing GMP that can be adapted for different throwing situations. This GMP contains the fundamental organizational principles that make all throwing movements recognizably similar while still allowing for the specific adaptations needed for different objects, distances, and targets.

The function of the GMP is to serve as the basis for generating movement instructions both prior to and during the performance of an action. This means that the GMP doesn’t just provide a rigid sequence of muscle commands, but rather a flexible framework that can be modified in real time to meet the specific demands of each movement situation. This flexibility is what allows us to perform familiar movements in new contexts while maintaining their essential characteristics.

16 GMP Characteristics

• Invariant features:
  • Characteristics that do not vary across performances of a skill within class of actions
  • The identifying signature of a GMP
• Parameters:
  • Specific movement features added to invariant features to adapt to a specific situation
  • Characteristics can vary from one performance of a skill to another

Let’s dive deep into motor program-based theory, specifically focusing on what’s called Schema Theory, developed by Richard Schmidt. To overcome the limitations of earlier motor program theories and account for the adaptive and flexible nature of human movement, Richard Schmidt (1975) proposed the generalized motor program (GMP). At the heart of this theory is the concept of the generalized motor program, which Schmidt proposed as a hypothesized memory-based mechanism responsible for the adaptive and flexible qualities of human movement. Now, you might wonder why Schmidt called it “generalized” rather than just a motor program. The key insight here is that Schmidt recognized a major limitation in earlier motor program theories - they suggested that we store separate programs for every specific movement we might ever perform. Think about how impractical this would be. Would you really need a separate motor program for throwing a ball to a target 10 feet away versus 12 feet away? That would require storing millions of slightly different programs! Schmidt’s brilliant solution was to propose that each GMP controls a class of actions that share common, fundamental characteristics. So instead of having separate programs for every possible throwing distance and direction, you have one generalized throwing program that can be adapted for different situations. The GMP’s primary function is to serve as the foundation for generating movement instructions both prior to and during the performance of an action. This allows for both the consistency we see in skilled movement patterns and the flexibility needed to adapt those patterns to varying environmental demands. This concept revolutionized our understanding of how the nervous system might efficiently organize and control the vast repertoire of movements humans can perform.

17 Invariant Features and Parameters Example

• Example of an invariant feature: Relative time of the components of a skill (i.e. % of total time each component uses)
• Example of a parameter: Overall amount of time taken to perform a skill

To understand how generalized motor programs work, we need to explore their key characteristics, which Schmidt organized into two essential components: invariant features and parameters. Invariant features are the characteristics that do not vary from one performance of a skill to another within a class of actions. Think of these as the “signature” or identifying characteristics of a GMP - they’re what makes a throwing movement recognizable as throwing, regardless of whether you’re throwing a baseball to first base or tossing a crumpled paper into a wastebasket. These invariant features form the core identity of the motor program and remain consistent across all variations of that movement class. They represent what is actually stored in memory as part of the GMP. On the other hand, parameters are the specific movement features that can be added to the invariant features to adapt the movement to a particular situation. These characteristics can and do vary from one performance of a skill to another. Parameters allow the same basic motor program to be customized for different environmental demands and task requirements. For example, when you’re throwing that baseball versus tossing the paper, the fundamental throwing pattern (the invariant features) remains the same, but the parameters - such as the amount of force applied, the overall speed of movement, and which specific muscles are emphasized - can be adjusted to meet the specific demands of each situation. This elegant system allows for both consistency and adaptability in human movement, solving the storage problem that plagued earlier motor program theories.

18 Analogy from Music and Dance

• Relative time = Rhythm (beat) of the music, (e.g. The 3 beats to a measure for a waltz)
• Overall time = Tempo (The speed at which you waltz)
• Regardless of how fast or slow you waltz, the rhythm remains the same (i.e. invariant)

Fig. 18.0: Dancers performing a waltz at different tempos - the same 3/4 time signature but different tempo markings.

To help you really grasp the concept of invariant features and parameters, let’s use a beautiful analogy from music and dance that makes these abstract concepts much more concrete. Think about a waltz - you know, that elegant ballroom dance with its distinctive “one-two-three, one-two-three” rhythm. In musical terms, this corresponds to a 3/4 time signature, meaning there are three beats to every measure of music. Now here’s the key insight: the relative time of a waltz corresponds to its rhythm or beat pattern. This rhythm represents the invariant feature - it’s what makes a waltz recognizable as a waltz, whether the music is played slowly for beginners learning the steps or quickly for experienced dancers showing off their skills. The rhythm - that fundamental “one-two-three” pattern - never changes. However, the overall time, which corresponds to the tempo or speed at which you waltz, represents a parameter that can be varied. You might waltz slowly and romantically to a gentle ballad, or more quickly and energetically to a livelier piece, but regardless of the tempo, that essential 3/4 rhythm remains constant. The beauty of this analogy is that it helps you understand how motor programs work in human movement. Just as a waltz maintains its characteristic rhythm across different tempos, a motor skill maintains its characteristic relative timing across different speeds of performance. Whether you’re walking slowly along a beach or hurrying to catch a bus, the fundamental timing relationships between the phases of your walking gait remain remarkably consistent - only the overall speed changes.

19 Illustration of Invariant Relative Time

• Demonstrates how relative timing remains consistent across different performance speeds
• Shows the fundamental principle of motor program theory

Fig. 19.0: A graph or chart showing movement phases plotted against time for the same skill performed at different speeds, with consistent relative timing percentages highlighted to show the invariant nature of the temporal structure.

Now let’s examine a visual representation of how invariant relative time works in practice. The illustration shows a hypothetical four-component motor skill performed at three different speeds, and it beautifully demonstrates the core principle of motor program theory. In this example, we can see the same motor skill performed normally at 10 seconds duration, speeded up to 5 seconds, and slowed down to 15 seconds. The fascinating thing to observe is that while the total duration changes dramatically, the relative timing of each component remains perfectly constant. Component A always takes 30% of the total time, Component B always takes 20%, Component C consistently requires 40%, and Component D invariably uses 10% of the total movement time. This consistency in relative timing is what motor program theorists argue represents the fundamental signature of a generalized motor program. Think about what this means for motor learning and control. It suggests that when you learn a new skill, you’re not just learning the specific muscles to contract or the exact forces to apply - you’re learning a temporal template that organizes the timing relationships between different phases of the movement. This template then serves as the foundation that can be scaled up or down in overall speed while preserving the essential coordination pattern. This concept has profound implications for motor skill instruction and rehabilitation. It suggests that when teaching a new skill, emphasis should be placed on helping learners establish the correct relative timing patterns, as these form the stable foundation that can then be adapted to different performance speeds and conditions.

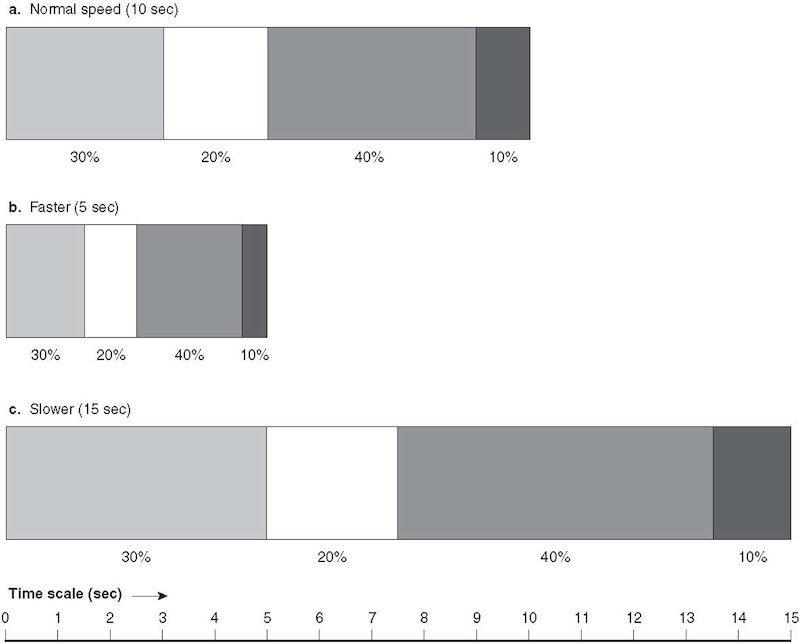
20 Testing Relative Time Invariance (Shapiro et al., 1981)

• Used gait characteristics to test prediction of relative time invariance for a class of actions controlled by a GMP
• Research question: Are walking and running one or two classes of action?
• Assessed 4 components of 1 step cycle
• Calculated relative time for each component at 9 speeds (3 – 12 km/hr)
• Relative time = % of total time for each component in 1 step cycle

Fig. 19.0: A graph or chart showing movement phases plotted against time for the same skill performed at different speeds, with consistent relative timing percentages highlighted to show the invariant nature of the temporal structure.

Let’s examine a fascinating research study that tested the concept of relative time invariance in real human movement. Shapiro, Zernicke, Gregor, and Diestel conducted a landmark experiment in 1981 that used gait characteristics to test a specific prediction of motor program theory. Their research question was particularly intriguing: Are walking and running controlled by one generalized motor program or two separate ones? This might seem like a simple question, but it gets to the heart of how motor programs are organized. To investigate this, the researchers had participants walk and run on a treadmill at nine different speeds, ranging from 3 to 12 kilometers per hour. They carefully analyzed four distinct components of one complete step cycle - essentially breaking down the walking and running patterns into their fundamental phases. For each speed condition, they calculated the relative time for each component, determining what percentage of the total step cycle time each phase required. Remember, if relative time is truly an invariant feature of a motor program, then these percentages should remain constant within each gait pattern, regardless of speed. The researchers were essentially asking: Does each component of the step cycle maintain the same proportion of total time as speed increases, and do walking and running show the same or different relative timing patterns? This experimental design was brilliant because it directly tested one of the key predictions of motor program theory while using a fundamental human movement that everyone can relate to. The results of this study provided crucial evidence about how motor programs might be organized in the human nervous system.

21 Shapiro et al. (1981) Results

• Relative time similar within speeds when walking but different from speeds when running
• Similar relative time within speeds when running
• Suggests walking and running are controlled by different GMPs

Fig. 21.0: Graphical representation of relative time invariance results, showing distinct patterns for walking and running across different speeds.

The results of the Shapiro study provided compelling evidence for motor program theory and revealed something fascinating about how walking and running are controlled. The researchers found that relative time was indeed similar within speeds when participants were walking, and it remained similar within speeds when they were running. This means that as walking speed increased from slow to fast, the relative timing of the different phases of the step cycle stayed remarkably consistent. The same pattern held true for running - whether participants were running slowly or quickly, the relative timing patterns remained stable. However, here’s the crucial finding: the relative time percentages were significantly different between walking and running gaits. When the researchers compared the timing patterns of walking versus running, they discovered that these two forms of locomotion showed distinctly different relative timing characteristics. This finding led to a important conclusion about motor program organization. The results suggested that walking and running gaits are controlled by two different generalized motor programs, each with its own characteristic invariant relative time structure. Think about what this means: your nervous system apparently has separate motor programs for walking and running, each with its own temporal signature. When you transition from walking to running - say, when you start jogging to catch a bus - you’re not just speeding up the same program. Instead, you’re switching from one motor program with its specific timing pattern to a completely different motor program with its own distinct timing characteristics. This finding has important implications for understanding motor control, gait rehabilitation, and how we might train different forms of locomotion.

22 Dynamical Systems Theory

• Describes the control of coordinated movement by emphasizing the role of environmental information and dynamic properties of the body/limbs
• Began to influence views about motor control in early 1980s
• Views the process of human motor control as a complex system that behaves like any complex biological or physical system
• Concerned with identifying laws (natural and physical) that govern emergence and change in human coordination patterns

Now let’s explore a completely different approach to understanding motor control - dynamical systems theory. This theory emerged in the early 1980s and represents a fundamental shift in thinking about how coordinated movement is controlled. Unlike motor program theory, which emphasizes memory-based mechanisms and central control, dynamical systems theory focuses on the role of environmental information and the dynamic properties of the body and limbs in movement control and coordination. The core insight of this approach is that human motor control should be viewed as a complex system that behaves like any complex biological or physical system we observe in nature. Think about how a flock of birds maintains its formation without a central controller telling each bird exactly where to fly, or how water molecules organize themselves into different states - liquid, solid, or gas - based on temperature and pressure conditions. Dynamical systems theorists argue that human movement coordination emerges in similar ways, through the interaction of multiple factors rather than through centralized programming. This theory is particularly concerned with identifying the natural and physical laws that govern how coordination patterns emerge and change over time. Instead of asking “What motor program controls this movement?” dynamical systems theorists ask “What conditions and constraints lead to the emergence of this coordination pattern?” This represents a profound shift from thinking about movement as executed programs to thinking about movement as emergent behavior that arises from the dynamic interaction between the person, the task, and the environment.

23 Concepts Based on Non-Linear Dynamics

• Behavioral changes are not always continuous - linear progressions - but are often sudden or abrupt
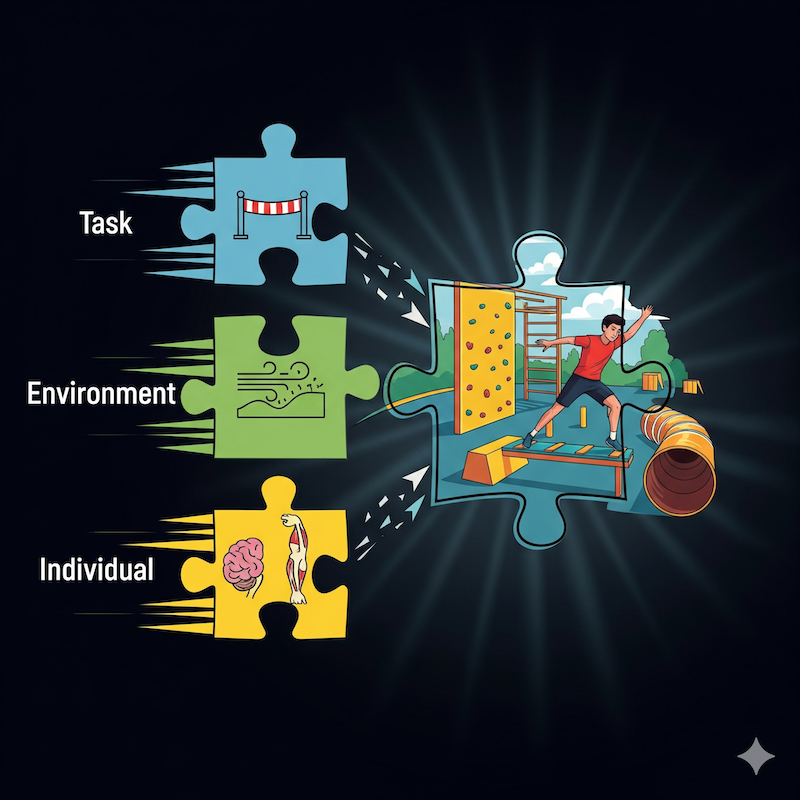
• Behavior is organized by the interactions among task, environmental, and organismic constraints
• Behaviors self-organize in response to constraints

Fig. 23.0: Behavioral changes can emerge from the interaction of constraints. On the left, a phase transition diagram shows how small changes in system parameters can lead to sudden shifts in behavior. On the right, a constraints model illustrates how task, environmental, and organismic factors overlap to produce emergent behaviors.

A key foundation of dynamical systems theory rests on concepts from non-linear dynamics, which reveal some fascinating principles about how complex systems behave. The first crucial concept is that behavioral changes are not always continuous, linear progressions - instead, they are often sudden or abrupt. This is quite different from what we might intuitively expect. In many systems, small, gradual changes in conditions can suddenly trigger dramatic shifts in behavior. Think about water being heated gradually - it stays liquid as temperature increases slowly, but then suddenly and dramatically changes to vapor at the boiling point. This type of sudden transition, called a phase transition, is characteristic of complex systems and appears frequently in human movement. The second fundamental concept is that behavior is organized by the interactions among three types of constraints: task constraints, environmental constraints, and organismic constraints. Task constraints refer to the specific demands of what you’re trying to accomplish - the rules of the game, the goal of the movement, or the requirements of the activity. Environmental constraints include factors like the surface you’re moving on, wind conditions, or obstacles in your path. Organismic constraints involve your individual characteristics - your height, strength, flexibility, or current fatigue level. The third key concept is that behaviors self-organize in response to these interacting constraints. This means that coordination patterns emerge naturally from the constraints present in the situation, rather than being imposed by a central controller. No single constraint is more important than others; instead, the coordination pattern that emerges represents the most stable solution given all the constraints acting on the system.

24 Attractors

• Attractor – A stable state of the motor control system that represents preferred patterns of coordination (e.g. walking)
• Characteristics of an attractor:
  • Identified by order parameters (e.g., relative phase)
  • Control parameters (e.g., speed) influence order parameters
  • Minimum trial-to-trial performance variability
  • Stability – Retains present state despite perturbation
  • Energy efficient

Central to dynamical systems theory is the concept of attractors - stable states of the motor control system that represent preferred patterns of coordination. Think of an attractor as a coordination pattern that the system naturally gravitates toward, much like a ball rolling into a valley. Walking is a perfect example of an attractor state - it’s a coordination pattern that emerges naturally and feels stable and comfortable for most people under normal conditions. Attractors have several characteristic features that help us identify and understand them. First, they are identified by order parameters, which are variables that capture the essential features of the coordination pattern. The most common order parameter is relative phase, which describes how different body parts move in relation to each other. For example, when you walk normally, your arms and legs coordinate in a specific phase relationship - as your right leg swings forward, your left arm swings forward, creating a stable, cross-lateral pattern. Second, attractors are influenced by control parameters - variables that, when changed, can affect the stability and character of the coordination pattern. Speed is a common control parameter. As you increase your walking speed, the basic walking pattern remains stable until you reach a critical point where it suddenly becomes more efficient to switch to running. Third, attractors show minimum trial-to-trial performance variability - when you’re in a stable attractor state, your movement pattern is consistent from step to step. Fourth, attractors demonstrate stability, meaning they resist change and tend to return to their preferred state even when briefly disturbed. Finally, attractors are energy efficient - the coordination patterns we naturally adopt tend to minimize energy expenditure for the task at hand.

25 Order and Control Parameters (1)

• Order parameters:
  • Also called collective variables
  • Variables that define the overall behavior of the system
  • Enable a coordinated pattern of movement to be distinguished from other patterns
  • Relative phase is the most prominent order parameter: It shows how one joint/segment moves relative to another

To understand dynamical systems theory better, we need to explore two crucial concepts: order parameters and control parameters. Order parameters, also called collective variables, are functionally specific variables that define the overall behavior of the system and enable us to distinguish one coordinated pattern from another. Think of order parameters as the key measurements that capture the essence of how different parts of the body are working together. The most prominent order parameter in rhythmic movements is relative phase, which describes the timing relationship between different moving parts. For instance, when you’re clapping your hands rhythmically, the relative phase describes whether your hands are moving in perfect synchrony (in-phase, with a relative phase of 0 degrees) or in perfect alternation (antiphase, with a relative phase of 180 degrees). In walking, relative phase might describe how your left and right legs coordinate, or how your arms coordinate with your legs. This measurement tells us not just that parts are moving, but how they’re moving relative to each other. Relative phase is particularly useful because it captures the coordination relationship in a single number that can be tracked over time. When relative phase remains stable, it indicates that the coordination pattern is consistent. When relative phase changes, it signals that the coordination relationship is shifting, perhaps indicating a transition to a different movement pattern. This makes relative phase an excellent window into understanding how coordination patterns are organized and how they change under different conditions.

26 Order and Control Parameters (2)

• Control parameter:
  • A variable, when increased or decreased, will influence the stability and character of the order parameter
  • Important to identify since it becomes the variable to manipulate to assess the stability of the order parameter
  • Provides the basis for determining attractor states for patterns of limb movement

Control parameters are variables that, when increased or decreased, will influence the stability and character of the order parameter. Understanding control parameters is crucial because they become the variables that researchers and practitioners can manipulate to assess the stability of coordination patterns and to promote changes in movement behavior. Control parameters don’t directly specify the coordination pattern - instead, they create the conditions under which different coordination patterns become more or less stable. Think of a control parameter as a “knob” that you can turn to influence how the system behaves, but the specific pattern that emerges depends on the complex interaction of all the constraints in the system. Speed is one of the most commonly studied control parameters in human movement. As you gradually increase your walking speed, the basic walking coordination pattern remains stable for a while. However, at a certain critical speed - different for each individual - the walking pattern suddenly becomes unstable and the system spontaneously transitions to running. The control parameter (speed) didn’t directly cause running; instead, it created conditions where running became the more stable, energy-efficient coordination pattern. Other examples of control parameters include task constraints like load (carrying a heavy backpack changes your gait), environmental constraints like surface texture (walking on sand versus concrete), or organismic constraints like fatigue level. The power of identifying control parameters lies in understanding what variables are most influential for creating behavioral change. This provides the basis for determining attractor states for patterns of limb movement and offers practical guidance for motor learning and rehabilitation interventions.

27 Self-Organization

• Behavior that spontaneously emerges in response to a particular set of constraints
• No one constraint is any more important than another in determining how the behavior is organized

Fig. 27.0: Self-organization of movement patterns.

One of the most fascinating concepts in dynamical systems theory is self-organization - the idea that coordinated behavior spontaneously emerges in response to a particular set of constraints without being directed by a central controller. This is quite different from the motor program approach, which suggests that coordination patterns are imposed by pre-existing programs stored in memory. Self-organization means that movement patterns arise naturally from the interaction of multiple factors, and importantly, no one constraint is any more important than another in determining how the behavior is organized. To understand self-organization, imagine you’re at a busy intersection without traffic lights. Initially, the flow of cars, bicycles, and pedestrians might seem chaotic. However, after a short time, you’ll often observe that organized patterns emerge spontaneously. Cars might naturally form lanes, pedestrians might cluster into groups that cross together, and cyclists might find optimal paths through the traffic. No single authority is directing this organization - instead, it emerges from the interaction of multiple constraints: the physical layout of the intersection, the number and types of travelers, their destinations, their preferred speeds, and the implicit social rules about giving way to others. This same principle applies to human movement coordination. When you’re walking on an icy sidewalk, your coordination pattern changes dramatically compared to walking on dry pavement. No central program tells you to adopt a different walking pattern; instead, a new coordination pattern self-organizes in response to the changed environmental constraints, combined with your organismic constraints (balance, strength, experience) and task constraints (getting to your destination safely).

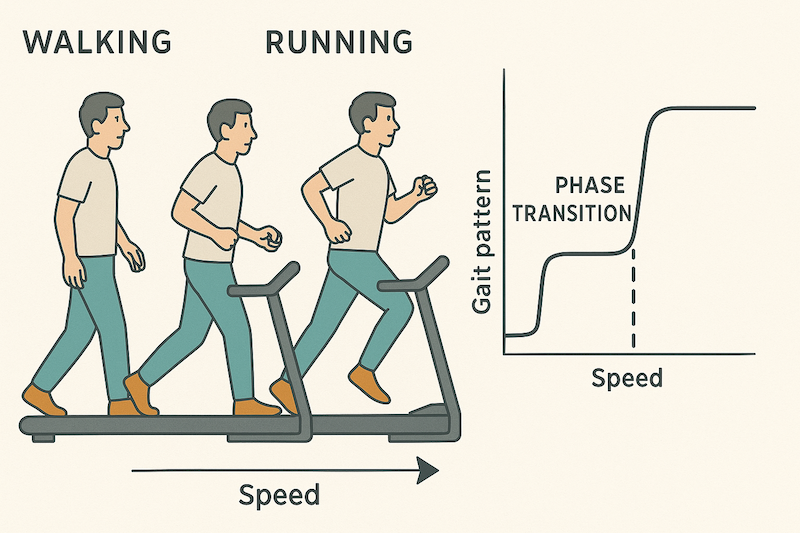
28 Examples of Self-Organization - Gait Transitions

• A person begins walking on treadmill at a slow speed
• Treadmill speed (control parameter) increases gradually
• Person shifts to running at a certain speed [not same speed for all people]
• Same effect if person begins running on treadmill - shifts to walk at certain speed

Fig. 28.0: Gait transitions on a treadmill.

Let’s examine a classic example of self-organization in human movement: gait transitions. Imagine you’re on a treadmill that starts at a slow walking speed. As the treadmill speed gradually increases, something fascinating happens. Initially, you simply walk faster while maintaining the same basic walking coordination pattern - your walking gait remains stable even as the speed increases. However, as the treadmill continues to speed up, you’ll reach a critical point where maintaining the walking pattern becomes increasingly difficult and inefficient. Suddenly, almost without conscious decision, you’ll find yourself transitioning to a running gait. This transition doesn’t happen because a central controller decided it was time to switch programs. Instead, it represents a beautiful example of self-organization in action. The walking coordination pattern becomes unstable when the control parameter (treadmill speed) reaches a critical value, and a new, more stable coordination pattern (running) spontaneously emerges. What makes this even more interesting is that this transition point isn’t the same for everyone - different people transition from walking to running at different speeds, depending on their individual constraints like leg length, fitness level, and movement experience. The same phenomenon occurs in reverse: if you start running on a treadmill and gradually decrease the speed, you’ll eventually reach a point where you spontaneously transition back to walking. These gait transitions demonstrate how coordination patterns can change suddenly and automatically in response to changing constraints, without requiring conscious control or pre-programmed instructions about when and how to make the switch.

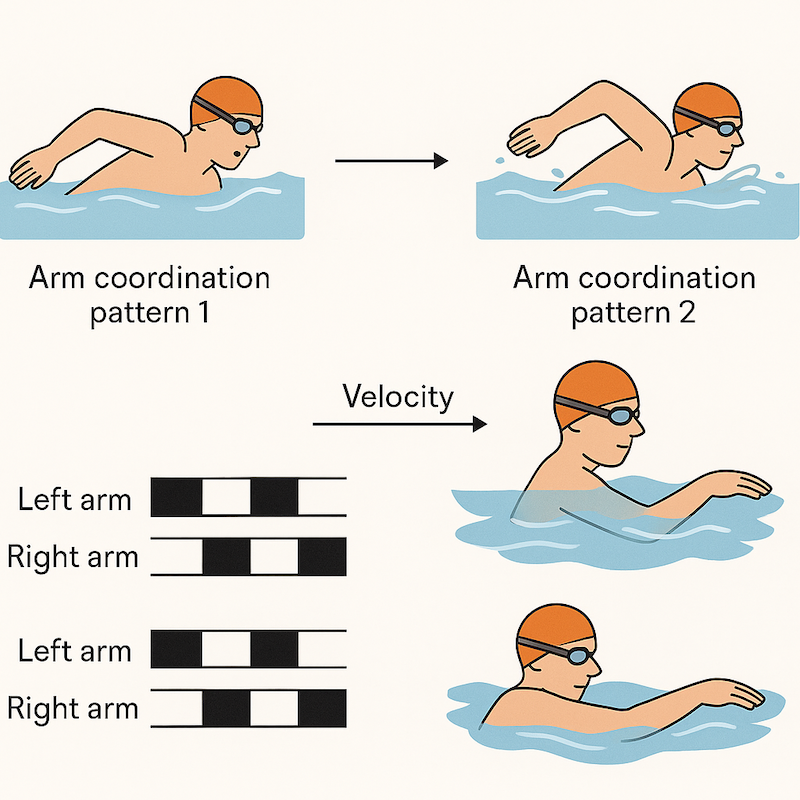
29 Examples of Self-Organization - Swim Stroke Transitions

• Seifert, Chollet & Bardy (2004)
• Each trial involved a swim velocity increase [began at preferred velocity]
• Arm-stroke analysis showed 2 distinct patterns of arm coordination
• Began in one mode but abruptly shifted to 2nd mode at a specific swim velocity

Fig. 29.0: Swim stroke transitions.

Another compelling example of self-organization comes from swimming research conducted by Seifert, Chollet, and Bardy in 2004. These researchers studied what happens to arm coordination patterns when swimmers are asked to gradually increase their swimming velocity, starting from their preferred, comfortable pace. The experimental design was elegant in its simplicity: swimmers began each trial at their naturally preferred velocity and then progressively increased their speed throughout the trial. Using detailed arm-stroke analysis, the researchers discovered that swimmers exhibited two distinct patterns of arm coordination. Initially, swimmers used one coordination mode, but as velocity continued to increase, they abruptly shifted to a second, different coordination mode at a specific swimming velocity. This transition wasn’t gradual or conscious - it happened suddenly when the velocity reached a critical threshold. What makes this study particularly fascinating is that it demonstrates self-organization in a complex, skilled movement performed in a fluid environment. The swimmers weren’t told when or how to change their coordination patterns. Instead, as the constraint of increased velocity made their original coordination pattern less stable or efficient, a new pattern spontaneously emerged. This research beautifully illustrates how coordination patterns can reorganize themselves in response to changing task demands. The swimmers’ motor systems automatically found new solutions that were more appropriate for the increased velocity demands. This type of spontaneous reorganization is exactly what dynamical systems theory predicts - that coordination patterns will naturally evolve and adapt as constraints change, without requiring explicit programming or conscious control of every aspect of the movement.

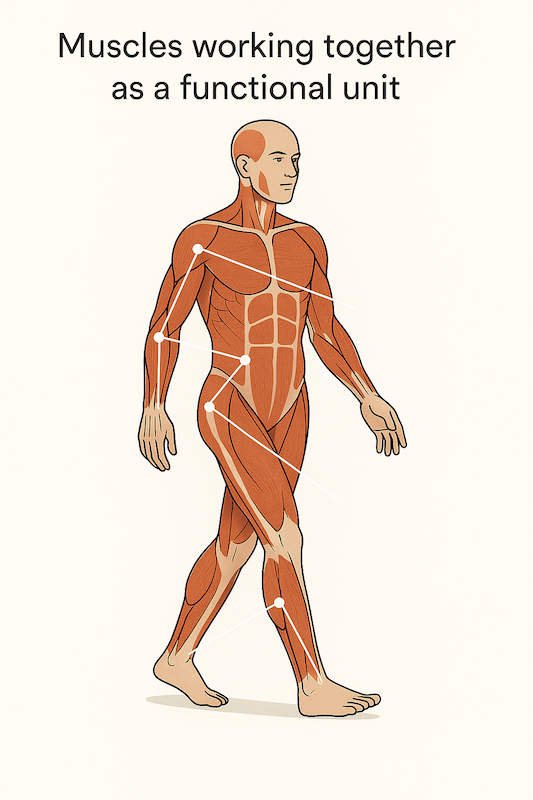
30 Coordinative Structures (Muscle Synergies)

• Groups of muscles (and joints) constrained to act as functional units
• If a perturbation stops one set of muscles from working, another automatically compensates
• Example: walking with a leg in a cast
• Develop through practice, experience, or naturally
• What are some other examples?

Fig. 30.0: Coordinative structures in action.

Now let’s explore how dynamical systems theory addresses the degrees of freedom problem through the concept of coordinative structures, also known as muscle synergies. Remember that the degrees of freedom problem asks how the nervous system manages to control the enormous number of independent muscles, joints, and limbs to produce coordinated movement. Coordinative structures offer an elegant solution to this challenge. A coordinative structure consists of groups of muscles and joints that are constrained by the nervous system to act as functional units. Instead of controlling hundreds of muscles independently, the nervous system organizes them into cooperative groups that work together toward a common goal. Think of this like conducting an orchestra. Rather than giving individual instructions to every single musician, a conductor organizes musicians into sections - the string section, the brass section, the woodwinds - and coordinates these sections to create beautiful music. Similarly, coordinative structures allow the nervous system to manage complexity by creating functional groupings. What makes coordinative structures particularly remarkable is their adaptive flexibility. If a perturbation stops one set of muscles from working properly, other muscles within the coordinative structure automatically compensate to maintain the intended function. A perfect example is what happens when you walk with a leg in a cast. You don’t consciously reprogram every muscle; instead, your motor system automatically reorganizes to create a new coordinative structure that accomplishes the goal of walking despite the constraint. Coordinative structures can develop through practice and experience, like learning to play a musical instrument, or they can emerge naturally, like the cross-lateral arm-leg coordination we see in normal walking. This concept helps explain how we can perform complex movements efficiently while maintaining the flexibility to adapt when conditions change.

31 A Coordinative Structure

• Demonstrates functional muscle groupings
• Shows automatic compensation mechanisms
• Illustrates flexibility within constraints

Fig. 31.0: A coordinative structure in action.

Coordinative structures represent one of the most elegant solutions to the degrees of freedom problem in motor control. These functional muscle groupings demonstrate how the nervous system organizes multiple muscles and joints to work together as cohesive units, rather than controlling each element independently. This organization dramatically simplifies motor control by reducing the number of elements that need to be actively managed. A key feature of coordinative structures is their automatic compensation mechanisms. When one muscle within the structure is compromised or unable to contribute fully, other muscles in the grouping can automatically adjust their activity to maintain the overall movement goal. This redundancy and flexibility ensure that movement can continue even when some components face constraints or limitations. Perhaps most importantly, coordinative structures illustrate flexibility within constraints. While these structures provide stable, reliable coordination patterns, they are not rigid. They can adapt their internal organization based on task demands, environmental conditions, or changes in the individual’s capabilities. This balance between stability and flexibility makes coordinative structures highly functional for meeting the diverse movement challenges we encounter in daily life. This concept helps explain how we can maintain effective movement patterns even as we age, experience fatigue, or face minor injuries - the coordinative structure adapts while preserving the essential movement function.

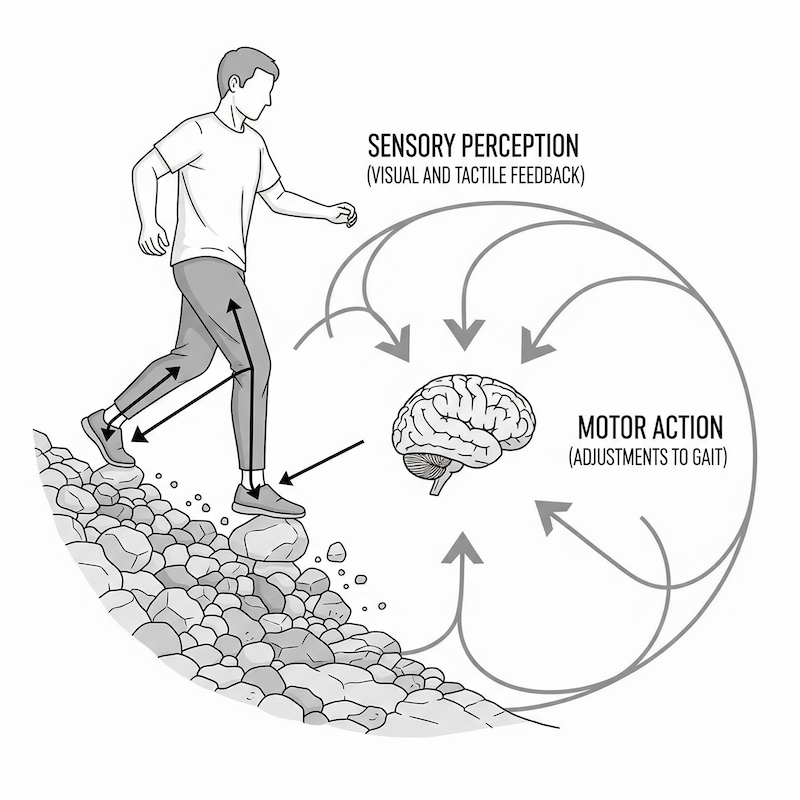
32 Perception-Action Coupling (1)

• The linking together (i.e., coupling) of information and actions/movements
• The perception part:
  • The detection and utilization of critical information for the control of action
• The action part:
  • The various movements that are regulated by the perceived information

Fig. 32.0: Perception-action coupling.

Perception-action coupling is a core idea in dynamical systems theory, describing how information from the environment and our movements are tightly linked in a continuous loop. The image on this slide likely shows a person interacting with their surroundings—perhaps reaching for an object, stepping over something, or responding to a visual cue. Arrows or lines may illustrate the flow of information: sensory input from the environment is perceived, which then guides the person’s movement, and those movements in turn generate new sensory information. This cycle repeats, showing that perception and action are not separate processes but are constantly influencing each other. Rather than passively observing the world, our perceptual systems actively pick up information that is directly relevant for guiding our actions. The image helps visualize this ongoing exchange, emphasizing that effective movement depends on this real-time connection between what we perceive and how we act.

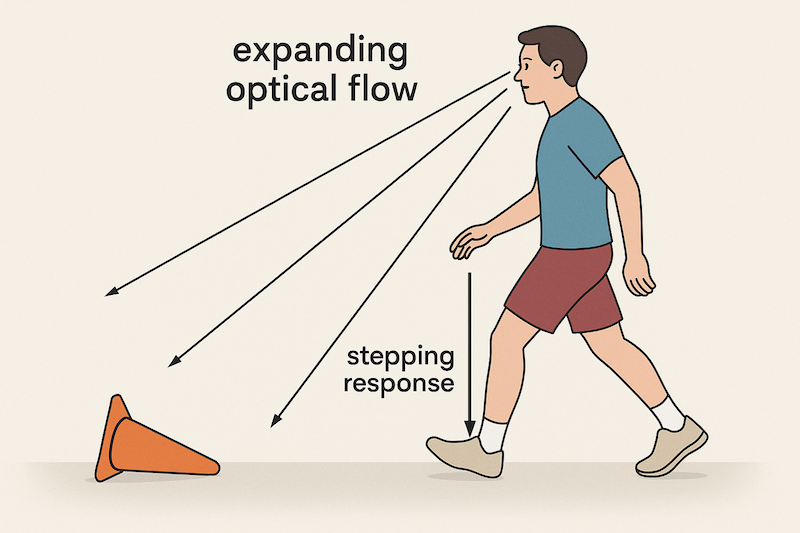
33 Perception-Action Coupling (2)

• An example:
  • When walking, the time to contact an object in your pathway (specified by the perceived rate of change of the object’s size) determines when you initiate stepping over the object
  • Your stepping action is “coupled” with your visual perception of the approaching object

Fig. 33.0: Perception-action coupling example.

Let me give you a concrete example that beautifully illustrates perception-action coupling in everyday movement. When you’re walking and encounter an object in your pathway - let’s say a fallen branch on a hiking trail - your visual system doesn’t just detect that there’s an obstacle present. Instead, it specifically picks up information about the time to contact with that object, which is specified by the perceived rate of change of the object’s size in your visual field. As you approach the branch, it appears to expand in your vision at a rate that directly corresponds to how quickly you’re approaching it. This expanding optical pattern provides your nervous system with precise information about when you’ll reach the obstacle. Here’s where the coupling becomes evident: this visual information about time to contact directly determines when you initiate your stepping-over action. You don’t consciously calculate the distance, estimate your walking speed, and then decide when to step over. Instead, your stepping action is directly “coupled” with your visual perception of the approaching obstacle. The visual information automatically triggers the appropriate timing for your avoidance movement. This is a perfect example of how perception and action work together as an integrated system rather than as separate, sequential processes. Your visual perception of the expanding object directly guides the timing of your motor response, and your stepping action simultaneously generates new visual information as you move through the environment. This continuous coupling allows for the smooth, automatic adjustments we make constantly while navigating through our complex, dynamic world.

34 Affordances

• Possibilities for action
• The reciprocal fit between characteristics of the person and the environment that allow certain actions to happen
• Example: the ratio of leg length to stair height determines whether a set of stairs is climbable

Fig. 34.0: A depiction of affordances.

The final concept from dynamical systems theory that we need to understand is affordances - a fascinating idea that describes the possibilities for action that exist in the relationship between a person and their environment. Affordances represent the reciprocal fit between characteristics of the person and characteristics of the environment that allow certain actions to happen. The key insight here is that affordances are not properties of the environment alone, nor are they properties of the person alone. Instead, they emerge from the relationship between the two. A classic example that illustrates this concept perfectly is the relationship between leg length and stair height. Whether a set of stairs is “climbable” depends not just on the height of the steps, but on the relationship between step height and the climber’s leg length. For a tall adult, steps that are 8 inches high might afford comfortable climbing, while the same steps might not afford climbing for a small child - they might instead afford crawling up on hands and knees. Interestingly, steps that are 15 inches high might not afford normal climbing for anyone, instead requiring a different action like stepping up and then stepping the other foot up to the same step. The environment hasn’t changed - the steps are the same height in all cases - but the affordances are different because of the different person-environment relationships. This concept has profound implications for understanding motor control and motor learning. It suggests that people don’t just learn movements in abstract; they learn to perceive and act on the affordances available in their environment. When designing training programs or rehabilitation interventions, understanding affordances helps us create environments that provide appropriate action possibilities for each individual’s capabilities.

35 Present State of the Control Theory Issue

• Currently, both the motor program-based theory and dynamical systems theory predominate
• Research investigating each has shown that a theory of motor control cannot focus exclusively on movement information specified by the CNS
• Task and environmental characteristics must also be taken into account
• Speculation exists that a hybrid of the two theories as a compromise theory could emerge to explain the control of coordinated movement

Fig. 35.0: Hybrid motor control theory.

As we near the end of our exploration of motor control theories, it’s important to understand where the field stands today regarding these competing perspectives. The present state of the control theory issue is both fascinating and complex, reflecting the ongoing evolution of scientific understanding in this dynamic field. Currently, both motor program-based theory and dynamical systems theory predominate in motor control research and application. Rather than one theory definitively winning out over the other, we’re seeing a period where both approaches contribute valuable insights to our understanding of human movement control. This coexistence isn’t a sign of confusion in the field, but rather a recognition that motor control is sufficiently complex to require multiple theoretical perspectives. What’s particularly interesting is that research investigating each theory has revealed important limitations when either approach is taken to an extreme. Studies have consistently shown that a theory of motor control cannot focus exclusively on movement information specified by the central nervous system, as purely motor program-based approaches might suggest. Similarly, purely environmental or dynamical approaches fall short when they don’t account for the sophisticated planning and memory capabilities of the nervous system. This research has led to a growing recognition that task and environmental characteristics must be taken into account regardless of which theoretical framework you favor. Even the most sophisticated motor programs must be flexible enough to adapt to changing environmental conditions, while even the most environmentally-driven movement patterns require some level of neural organization and control. Perhaps most intriguingly, there’s growing speculation among researchers that a hybrid approach - combining elements of both theories as a compromise theory - could emerge to provide a more complete explanation of how we control coordinated movement. Such a hybrid theory might recognize that different types of movements and different phases of skill acquisition might rely more heavily on one approach versus the other. This evolving theoretical landscape reflects the maturation of the field and suggests that future breakthroughs in understanding motor control will likely come from integration rather than competition between these approaches.

36 Takeways

• Motor control theories provide explanations about how the nervous system controls coordinated movement
• Coordination is the patterning of body and limb motions relative to environmental objects and events
• The degrees of freedom problem refers to how the nervous system controls the many degrees of freedom of muscles, limbs, and joints to enable a person to perform an action as intended
• Open-loop control systems do not use feedback, while closed-loop control systems do
• Motor program-based theory emphasizes memory-based mechanisms for controlling movement, while dynamical systems theory emphasizes the role of environmental information and mechanical properties of the body and limbs
• Both theories contribute to our understanding of motor control and may be integrated in future research

As we wrap up our exploration of motor control theories, let’s take a moment to consolidate the key concepts we’ve covered today. These takeaways represent the essential insights that will serve as the foundation for your understanding of how the nervous system controls coordinated movement. First and foremost, motor control theories provide crucial explanations about how our incredibly complex nervous system manages to control coordinated movement. These theories don’t just describe what happens - they help us understand the underlying mechanisms and principles that make skilled movement possible. This theoretical foundation is essential for anyone working in fields related to human movement, whether you’re a future physical therapist, athletic trainer, or sports coach. We’ve learned that coordination represents the patterning of body and limb motions relative to environmental objects and events. This isn’t just about moving individual body parts - it’s about how all the components of our movement system work together in organized, purposeful patterns that allow us to interact effectively with our environment. Understanding coordination helps us appreciate the remarkable complexity underlying even simple movements. The degrees of freedom problem highlights one of the most fundamental challenges in motor control: how does the nervous system manage to control the hundreds of degrees of freedom available in our muscles, limbs, and joints to enable us to perform actions as intended? This problem underscores the computational challenge our nervous system faces every moment and helps explain why motor control is such a fascinating area of study. We’ve explored two fundamentally different approaches to control systems. Open-loop control systems operate without feedback, relying on pre-programmed instructions, while closed-loop control systems continuously use feedback to guide and modify ongoing movement. Understanding these differences helps us appreciate the various ways our nervous system can control movement depending on the task demands and environmental constraints. The two major theoretical frameworks we’ve studied - motor program-based theory and dynamical systems theory - offer different but complementary perspectives on motor control. Motor program-based theory emphasizes memory-based mechanisms, suggesting that our nervous system stores and retrieves movement programs, while dynamical systems theory emphasizes the role of environmental information and the mechanical properties of our body and limbs in shaping movement patterns. Rather than viewing these as competing theories, current thinking suggests that both contribute valuable insights to our understanding of motor control, and future research may well integrate elements from both approaches to provide a more complete picture of how we control movement. These concepts aren’t just academic curiosities - they have direct implications for how we approach motor skill instruction, rehabilitation, and performance enhancement in real-world settings.

References

Haywood, K. M., & Getchell, N. (2024). Life span motor development (8th ed.). Human Kinetics.

Magill, R., & Anderson, D. I. (2017). Motor learning and control: concepts and applications (11th edition). McGraw-Hill Education.